{lang=EN}

This is a manual about JSXGraph.

(Work in progress)

JSXGraph is a cross-browser JavaScript library for interactive geometry, function plotting, charting, and data visualization in the web browser.

This book covers the basics, how to build simple constructions and also some advanced topics on how to include JSXGraph in Moodle.

To build JSXGraph constructions you don't need to be programmer (although it helps), but is rather more like putting together elements of the construction.

Below is an example of power of JSXGraph. Hint: Move the dot and observe. {/lang}

{lang=CZ}

Příručka pro práci v JSXGraphu.

(Na tomto díle se stále pracuje)

JSXGraph je knihovna JavaScriptu pro realizaci dynamické interaktivní geometrie, vykreslování funkcí, grafů a další vizualizace dat přímo ve webovém prohlížeči, nezávisle na jeho typu.

Tato příručka je věnována především úvodu do základních konstrukcí v JSXGraphu, nevyhýbá se však ani pokročilejším tématům, především v souvislosti se začleněním JSXGraphu do Moodle.

Chcete-li tvořit dynamické materiály v JSXGraphu, nemusíte být nutně programátorem (i když by Vám to samozřejmě pomohlo), ve většině případů práce připomíná spíše skládání prvků stavebnice.

Níže je uvedena ukázka možností JSXGraphu (Návod: Pohybujte posuvníkem - bodem na úsečce při dolním okraji okna a sledujte, co se děje). {/lang}

{lang=SI}

To je priročnik o JSXGraphu.

JSXGraph je knjižnica JavaScript v brskalniku za interaktivno geometrijo, risanje funkcij, grafikone in vizualizacijo podatkov v spletnem brskalniku.

Ta knjiga zajema osnove, kako zgraditi preproste konstrukcije in tudi nekatere napredne teme o tem, kako vključiti JSXGraph v Moodle.

Če želite zgraditi JSXGraph konstrukcije, vam ni treba biti programer (čeprav pomaga), ampak je bolj podoben sestavljanju elementov konstrukcije.

Spodaj je primer moči JSXGraph. Namig: premaknite piko in opazujte. {/lang}

{lang=DE}

Dies ist ein Handbuch zu JSXGraph.

(In Entstehung)

JSXGraph ist eine browser-unabhängige JavaScript-Bibliothek zu interaktiver Geometrie, Funktionsgraphen, Diagrammen und Daten-Visualisierung im Web-Browser.

Dieses Handbuch beschreibt die Grundlagen, wie einfache Konstruktionen erstellt werden können, sowie einige fortgeschrittenere Themen, zum Beispiel die Einbindung von JSXGraph in Moodle.

Um JSXGraph-Konstruktionen erstellen zu können, muss man kein Programmierer sein (obwohl es hilfreich ist); es ist mehr ein Zusammenstellen der Konstruktionselemente.

Das Beispiel unten zeigt die Mächtigkeit von JSXGraph. Hinweis: Bewegen Sie den Punkt und beobachten Sie was geschieht. {/lang}

{lang=EN}

How to setup

When we prepare JSX construction it is most convenient to prepare it locally. For that we have to create some file (eg. example.htm), copy paste template provided below and we can start constructing. After we save the program, we can open it in our favorite browser (Firefox, Chrome, etc). We can repeat the following: edit the file, save it and refresh it ((F5) in a browser) until we're satisfied with result.

Basic template for building and testing is below {/lang} {lang=CZ}

Jak začít

Když chceme vytvořit novou konstrukci v JSXGraphu, nejlepší je připravit si ji lokálně, ve svém počítači. Není nutné ji nahrávat na nějaký server, stačí, když ji uložíme formou HTML souboru do svého počítače a následně otevřeme v našem oblíbeném prohlížeči.

Níže je uveden vzor obsahu HTML souboru webové stránky pro tvorbu a testování JSX appletu. Stačí jednoduše vytvořit soubor, řekněme s názvem priklad.html, a zkopírovat do něj obsah níže uvedeného okna. Jediné, co potom budeme při tvorbě vlastního appletu měnit, je pasáž mezi tagy <script>, </script>.

Dokud nejsme spokojeni s podobou appletu, opakujeme následující akce: editace souboru, jeho uložení a prohlédnutí prohlížečem (zobrazení stránky v prohlížeči aktualizujeme stisknutím (F5)). {/lang} {lang=SI}

Namestitev

Ko pripravljamo JSX konstrukcijo, je najbolje, da jo shranimo lokalno. Za to ustvarimo nek dokument (npr primer.html), kopiramo in prilepimo spodnjo predlogo in začnemo s konstrukcijami. Ko dokument shranimo, ga odpremo v brskalniku (Firefox, Chrome, ...). Potem samo ponavljamo postopek: uredi, shrani, osveži spletno stran. Spodaj je predloga dokumenta za testiranje. {/lang} {lang=DE}

Vorbereitung

Eine JSXGraph-Konstruktion kann am bequemsten lokal mit einem Text-Editor auf einem Computer erstellt werden. Dazu legen wir eine leere HTML-Datei an (z.B. example.htm) und kopieren die untenstehende Vorlage in die Datei. Danach können wir mit dem Konstruieren beginnen. Nachdem wir die Datei gespeichert haben, können wir sie in einem Web-Browser unserer Wahl (Firefox, Chrome, etc) ansehen.

Dieser Prozess kann beliebig wiederholt werden: Datei bearbeiten, speichern und im Browser aktualisieren ((F5) im Web-Browser), so lange bis wir mit dem Resultat zufrieden sind.

Hier ist eine Vorlage für eine einfache HTML-Datei mit JSXGraph: {/lang}

<!DOCTYPE HTML>
<html lang="en">
  <head>
    <meta charset="UTF-8">
    <title>JSXGraph template</title>
    <meta content="text/html; charset=utf-8" http-equiv="Content-Type">
    <link href="https://cdn.jsdelivr.net/npm/jsxgraph/distrib/jsxgraph.css" rel="stylesheet" type="text/css" />
    <script src="https://cdn.jsdelivr.net/npm/jsxgraph/distrib/jsxgraphcore.js" type="text/javascript" charset="UTF-8"></script>
    <!-- The next line is optional: MathJax -->
    <script src="https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-chtml.js" id="MathJax-script" async></script>
  </head>
  <body>

  <div id="jxgbox" class="jxgbox" style="width:500px; height:200px;"></div>

  <script>
    var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-5, 2, 5, -2]});
  </script>

  </body>
</html>

{lang=EN} These scripts are all downloaded from the internet, therefore we need an constant internet connection. {/lang} {lang=CZ} Všechny použité skripty jsou nahrávány z internetu, proto je třeba mít trvalé internetové připojení. {/lang} {lang=SI} Ker so skripte prenesene z interneta, potrebujemo konstantno internetno povezavo. {/lang} {lang=DE} Diese Zusatzdateien werden alle aus dem Internet heruntergeladen, deshalb benötigen wir eine Internetverbindung. {/lang}

{lang=EN}

Basics

JSXGraph construction is composed from:

• drawing board
• objects (points, lines, etc.)
• relations between objects (optional, if we want some dynamics in the construction)
• events (optional, if we want some additional actions to be triggered)

In this section we will cover how to create drawing board, objects and use them to construct some simple examples.

{/lang}

{lang=CZ}

Základy

Konstrukce v JSXGraphu má tyto základní prvky:

• nákresna
• objekty (body, přímky atd.)
• vztahy mezi objekty (volitelné, chceme-li mít v konstrukci nějakou dynamiku)
• události (volitelné, pokud chceme, aby byly spuštěny nějaké doplňkové akce)

V této části příručky se budeme věnovat vytvoření nákresny a zobrazení základních objektů, jejichž užití si budeme ilustrovat prostřednictvím jednoduchých příkladů.

{/lang}

{lang=SI}

Osnove

JSXGraph kostrukcijo sestavljajo:

• risalna povšina
• objekti (točke, črte, itd.)
• relacije med objekti (če želimo dinamiko med objekti)
• dogodki (če želimo sprožiti kakšne dodatne akcije)

V tem poglavju bomo opisali, kako konstruirati risalno površino in točke na njej ter kako jih uporabiti za preproste konstrukcije.

{/lang}

{lang=DE}

Grundlagen

Jede JSXGraph-Konstruktion setzt sich zusammen aus:

• Zeichenfläche
• Objekten (Punkten, Geraden, etc.)
• Beziehungen zwischen Objekten (nur falls wir Dynamik in der Konstruktion benötigen)
• Ereignissen (events) (optional, falls zusätzliche Aktionen ausgelöst werden sollen)

In diesem Kapitel werden wir kennenlernen, wie eine Zeichenfläche angelegt wird und wie sie für einfache Beispiele genutzt werden kann.

{/lang}

{lang=EN}

Drawing area

JSXGraph needs canvas as a place to put constructions on. Because we have HTML and Javascript we need an element in HTML which we will tell Javascript to use as canvas. First we create a place in HTML where we will our construction be. For this we use div element with some properties.

<div id="jxgbox" class="jxgbox" style="width:500px; height:200px;"></div>

If we look at the line closely we see a few properties. For us it is important id="jxgbox" which we use to connect with JSXGraph. Next is class="jxgbox" where we can specify how our board will look like. This is more advanced topic and will be discussed later. Last property is style="width:500px; height:200px;" where we define size of our drawing board.
Important: here we do not define our coordinate system, but only the size of our canvas.

When we have defined our canvas, we have to connect them with JSXGraph. This is done with the following line, which should be put inside of a <script></script> tag.

var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-5, 2, 5, -2]});

We can see we called function initBoard, which constructs our drawing board . This function needs at least one argument, which is the id of the element div we defined in our example jxgbox. The text boundingbox: [-5, 2, 5, -2] sets the bounds for the coordinate system of our construction.

Observing both lines we see, that we have two measures for size. With div we created a canvas with the size in pixels. Then we declared a coordinate system and its size, which we will use to place objects on the board. {/lang}

{lang=SI}

Risalna površina

JSXGraph potrebuje platno kot prostor, kamor postavljamo našo konstrukcijo. Ker uporabljamo HTML in Javascript, potrebujemo element v HTML, ki pove Javascriptu, da uporabljamo platno. To storimo na naslednji način

<div id="jxgbox" class="jxgbox" style="width:500px; height:200px;"></div>

Opazimo lahko nekaj lastnosti. Za nas so pomembni id="jxgbox", s katerim se povežemo z JSXGraph. Naslednji je class="jxgbox", kjer določimo, kako bo naša površina izgledala. Gre za malo naprednješo temo in bo v podrobnosti opisana kasneje. Nazadnje imamo style="width:500px; height:200px;", s tem določimo velikost naše površine v pikslih.

Pomembno: tukaj ne definiramo koordinatnega sistema, ampak samo velikost platna.

Sedaj ga lahko povežemo z JSXGraph z naslednjo vrstico, ki jo moramo zapisati med simbola <script> </script>

var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-5, 2, 5, -2]});

Vidimo, da kličemo funkcijo z imenom initBoard, ki konstruira risalno površino. Ta funkcija potrebuje vsaj en argument, ki je ime oziroma identiteta id prej definiranega platna. V našem primeru je to jxgbox. V tem primeru smo uporabili še en agrument, to je boundingbox: [-5, 2, 5, -2], ki našemu platnu določi meje koordinatnega sistema.

{/lang}

{lang=CZ}

Nákresna

JSXGraph potřebuje nějakou zobrazovací plochu, nákresnu, na kterou může vykreslovat konstrukce. Jelikož využíváme HTML a Javascript, potřebujeme vytvořit prvek v HTML, který bude Javascript používat jako své plátno. Nejprve vybereme v HTML místo, kde bude naše konstrukce umístěna. K tomu využijeme blokový prvek <div>, kterému nastavíme potřebné atributy.

<div id="jxgbox" class="jxgbox" style="width:500px; height:200px;"></div>

Pokud se na řádek s kódem pozorně zaměříme, odhalíme několik nadefinovaných vlastností. Pro nás nejdůležitější je id="jxgbox", který slouží k identifikaci nákresny a její propojení s JSXGraph. Následuje class="jxgbox", což je přiřazení třídy, které slouží k nadefinování vzhledu naší nákresny. To je však pokročilejší téma, kterému se budeme věnovat později. Poslední vlastností je style="width:500px; height:200px;". Ta slouží k určení velikosti naší nákresny na webové stránce.

Důležité: Zde nenastavujeme podobu a polohu naší soustavy souřadnic, ale pouze velikost zobrazované nákresny.

Jakmile jsme si nadefinovali naší nákresnu, musíme ji propojit s JSXGraph. Toho dosáhneme následujícím řádkem, který však musíme umístit do prvku <script>, abychom jednoznačně určili, že se již jedná o samotný skript.

var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-5, 2, 5, -2]});

Vidíme, že jsme využili funkci initBoard, která po svém zavolání vytvoří naší nákresnu. Tato funkce pro správné fungování potřebuje alespoň jeden argument. V našem případě jsme jako argument použili id námi definovaného prvku <div> tj. jxgbox. Atribut boundingbox: [-5, 2, 5, -2] poté JSXGraph sděluje, jakou část systému souřadnic chceme pro svou konstrukci zobrazovat.

Pokud mezi sebou porovnáme oba řádky kódu, zjistíme, že pro nastavení velikostí využíváme dvě různé míry. Pomocí <div> jsme určili velikost nákresny v pixelech. Poté jsme na nákresně definovali systém souřadnic, který bude sloužit k umisťování objektů do nákresny. {/lang}

{lang=DE}

Zeichenbereich

JSXGraph benötigt eine Zeichenfläche, auf der die Konstruktion angelegt werden kann. Da die Konstruktion in einem Web-Browser mit Hilfe der Programmiersprache JavaScript angezeigt werden soll, müssen wir zuerst ein HTML-Element anlegen, das JSXGraph als Zeichenfläche verwenden kann. Dies geschieht, indem wir folgendes div-Element mit einigen Eigenschaften anlegen:

<div id="jxgbox" class="jxgbox" style="width:500px; height:200px;"></div>

Wenn wir diese Zeile genauer betrachten, sehen wir ein paar Besonderheiten. Besonders wichtig ist für unsere Zwecke das Attribut id="jxgbox", das wir nützen um die HTML-Seite mit JSXGraph zu verknüpfen. Als nächstes folgt class="jxgbox", womit wir festlegen, wie die Zeichenfläche aussieht. Das ist bereits ein Thema für Fortgeschrittenere und wird später diskutiert werden. Das letzte Attribut ist style="width:500px; height:200px;", das die Größe der Zeichenfläche festlegt.
Wichtig: damit legen wir nicht unser Koordinatensystem fest, sondern lediglich die Größe unserer Zeichenfläche.

Wenn wir nun so unsere Zeichenfläche in HTML festgelegt haben, können wir sie mit JSXGraph verknüpfen. Dies machen wir mit der folgenden Zeile, die innerhalb eines <script></script>-Befehls stehen muß:

var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-5, 2, 5, -2]});

In dieser Zeile wird die Funktion initBoardaufgerufen, die eine JSXGraph-Zeichenfläche anlegt. Diese Funktion erwartet mindestens ein Argument, nämlich die *id* des HTML-Elementsdiv`, die in unserem Beispiel den Wert jxgbox hat. Mit dem zweiten Argument {boundingbox: [-5, 2, 5, -2]} wird in JSXGraph das Koordinatensystem unserer Konstruktion festgelegt.

Vergleichen wir beide Zeilen, so erkennen wir zwei Größeneinheiten. Mit div wurde eine Zeichenfläche angelegt, deren Größe in Pixel angegeben ist. Mit initBoard haben wir zudem ein Koordinatensystem in unserer Zeichenfläche angelegt, das wir nutzen werden um Objekte auf der Zeichenfläche zu positionieren. {/lang}

{lang=EN}

Creating points

Points are one of the most basic objects in JSXGraph. We always create objects on the JSXGraph board, therefore we must use same board variable for the construction of all objects that will be on board. {/lang}

{lang=SI}

Risanje točk

Točke so eni izmed najbolj osnovnih objektov v JSXGraphu. Objekte vedno ustvarimo na risalni površini. {/lang}

{lang=CZ}

Vytváření bodů

Body jsou základními a nejjednoduššími objekty v JSXGraph. V tomto příkladu zakreslíme do nákresny dva body. {/lang}

{lang=DE}

Punkte erzeugen

Punkte gehören zu den grundlegendsten Objekten in JSXGraph. Wir legen alle Objekte auf die Zeichenfläche (genannt "board"), deshalb verwenden wir für alle Objekte, die auf dieser Zeichenfläche entstehen sollen, dieselbe Variable board. {/lang}

<div id="jxgbox" class="jxgbox" style="width:500px; height:200px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-5, 2, 5, -2]});
 board.create('point',[-2,1]);
 var q = board.create('point',[3,0]);
</script>

{lang=EN} Let us now observe board.create('point',[-2,1]);. Here we use variable board and call a method create which takes two arguments. First argument is the type of the object and second the coordinates where this object should be. If we define coordinates outside of the bounding box, the object will exist but won't be visible because it is outside visible area of our drawing board.

Next line var q = board.create('point',[3,0]); is very similar to the previous line, with only one difference. We start the line with var q = which we use to store this object in variable q. This is good and necessary practice, because in the constructions we often reference different object and define their relationships, which will be more apparent in following pages.

{/lang}

{lang=SI}

Opazujmo zapis board.create('point',[-2,1]);. Tukaj uporabimo spremenljivko board in kličemo metodo create, ki potrebuje dva argumenta. Prvi je tip objekta, drugi pa položaj, kjer se naj ta objekt nahaja. Če definiramo položaj, ki je izven našega koordinatnega sistema, bo objekt sicer obstajal, vendar ne bo viden na sliki.

Naslednja vrstica var q = board.create('point',[3,0]); je podobna prejšnji, z eno razliko. Zapis smo začeli z var q = , kar pomeni, da shranimo objekt v neko spremenljivko z imenom q. To je dobra praksa, saj se velikokrat v konstukcijah navezujemo na že prej definirane objekte, kar lahko storimo samo, če jih prej shranimo v spremenljivko. Primer te uporabe bo razložen v naslednjem poglavju.

{/lang}

{lang=CZ} Zaměřme se nyní na board.create('point',[-2,1]);. Zde využíváme proměnnou board a metodu create, která vyžaduje dva argumenty. Prvním argumentem určujeme, jaký typ objekt se má v nákresně vytvořit, což je v našem případě bod, point. Druhý argument určuje souřadnice, na kterých bude bod v nákresně sestrojen. Pokud použijeme souřadnice, které leží mimo námi nadefinovaný systém souřadnic, tak se bod stejně sestrojí. Vytvořený bod ale nebude na naší nákresně viditelný, neboť bude sestrojen mimo zobrazovanou plochu. Pohybem po nákresně pomocí zoomu a šipek v jejím pravém dolním rohu je však možné sestrojený bod objevit.

Další řádek var q = board.create('point',[3,0]); je velice podobný předchozí konstrukci pouze s jedním rozdílem. Naší konstrukci začínáme var q = . Toto přiřazení slouží obecně k ukládání objektů do proměnných. V naší ukázce sestrojený bod ukládáme do proměnné q.

Ukládání objektů do proměnných je dobrou a často nezbytnou praxí. V konstrukcích se budeme často odkazovat na existující objekty a definovat mezi nimi vztahy a to právě pomocí proměnných. Toto bude patrnější na následujících stránkách. {/lang} {lang=DE} Sehen wir uns den Befehl board.create('point',[-2,1]); genauer an: Wir verwenden die Variable board und rufen deren Methode create auf, die zwei Argumente hat.

Das erste Argument ist der Typ des Objekts, das wir anlegen wollen. Das zweite Argument legt fest wo das Objekt sein soll. Wenn wir Koordinaten außerhalb der Zeichenfläche angeben, wird das Ojekt zwar existieren, aber nicht sichtbar sein.

Die nächste Programmzeile var q = board.create('point',[3,0]); ist der vorhergehenden sehr ähnlich - mit einem wesentlichen Unterschied. Wir starten die Zeile mit var q = . Damit speichern wir dieses Objekt in der Variablen q. Das ist bewährte und notwendige Praxis, denn in unseren Konstruktionen werden wir oft auf bereits existierende Objekte zurückgreifen und ihre gegenseitigen Abhängigkeiten festlegen. Dies wird auf den folgenden Seiten klarer werden. {/lang}

{lang=EN}

Creating lines

Lines are the next type of objects that we will learn. Line is defined by two points through which a line is drawn. Here is an example of a board with two lines. {/lang}

{lang=SI}

Ustvarjanje premic

Premice so naslednji objekti, ki se jih bomo naučili. Premico definiramo z dvema točkama, skozi kateri poteka ravna črta. Tukaj je primer platna z dvema premicama. {/lang}

{lang=CZ}

Kreslení přímek

Dalším objektem, s jehož konstrukcí se seznámíme, je přímka. Ta je v JSXGraphu definována dvěma body, kterými prochází.

Níže je uveden příklad kódu, kterým jsou v nákresně narýsovány dvě přímky. První z nich je zadána přímo souřadnicemi určujících bodů, druhá je potom definována pomocí proměnných, které jsou jejím určujícím bodům přiřazeny.

{/lang}

{lang=DE}

Geraden erzeugen

Geraden sind der nächste Objekttyp, den wir kennenlernen. Eine Gerade wird durch zwei Punkte festgelegt. Hier ist ein Beispiel einer Zeichenfläche mit zwei Geraden: {/lang}

<div id="jxgbox" class="jxgbox" style="width:500px; height:200px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-5, 2, 5, -2]});
 var line1 = board.create("line",[[-3,1],[3,-1]]);

 var p = board.create('point',[-2,-1]);
 var q = board.create('point',[3,1]);
 var line2 = board.create("line",[p,q]);
</script>

{lang=EN} Result: {/lang}

{lang=CZ} Výsledek: {/lang}

{lang=DE} Resultat: {/lang}

{lang=SI} Rezultat: {/lang}

{lang=EN} Line of code var line1 = board.create("line",[[-3,1],[3,-1]]); creates line1 through two points [-3,1] and [3,-1]. For each point again we had to define $x$ and $y$ coordinate. Because for the line we need to provide a list of two points, we enclose both points in square brackets, therefore the list of two points is [[-3,1],[3,-1]].

For the second line2 we first defined two points $p$ and $q$ and used them as [p,q] when defining the line2. Here we already see why it is useful to store objects in variables, because now we could define another line, that could also go through point $p$ or $q$ and we don't need to worry if coordinates are correct.

Note: In Javascript lists are written in square brackets [ ]. {/lang}

{lang=SI} Premici smo ustvarili na dva načina. Vrstica var line1 = board.create("line",[[-3,1],[3,-1]]); ustvari črto z imenom line1 skozi dve točki s koordinatama [-3,1] in [3,-1]. Ker potrebujemo dva podatka, oziroma dve točki, moramo podatke našteti v seznamu, torej med oglate oklepaje []. Zato dobimo zapis [[-3,1],[3,-1]].

Za drugo premico line2 smo najprej definirali dve točki $p$ in $q$ in uporabili seznam [p,q] za definicijo line2. Tukaj lahko opazimo, zakaj je koristno shranjevati objekte v spremenljivke. Če želimo zapisati več različnih premic, ki grejo skozi eno izmed točk $p$ ali $q$, ne rabimo vsakič znova zapisovat koordinat teh dveh točk, saj sta točki že prej definirani.

Opomba: V Javascriptu se seznami pišejo v oglate oklepaje [ ]. {/lang}

{lang=CZ} Řádek s kódem var line1 = board.create("line",[[-3,1],[3,-1]]); vytváří přímku line1, která prochází body [-3,1] a [3,-1]. Každý bod je definován uspořádanou dvojicí (seznamem) souřadnic $x$ a $y$. Uspořádaný seznam je uzavřen do hranatých závorek [...]. Protože přímka je určena dvěma body, zapisujeme do její definice seznam těchto bodů[[-3,1],[3,-1]].

V případě druhé přímky line2 jsme nejprve definovali dva body $p$ a $q$ a v definici přímky použili jejich proměnné [p,q]. Již na tomto jednoduchém příkladě vidíme, jak je užitečné ukládat objekty do proměnných. Potom můžeme například klidně definovat třetí přímku, procházející některým z bodů $p$, $q$ a nemusíme se strachovat, zda jeho souřadnice opisujeme dobře.

Poznámka: V Javascriptu je seznam uváděn v hranatých závorkách [ ]. {/lang}

{lang=DE} Durch die Programmzeile var line1 = board.create("line",[[-3,1],[3,-1]]); wird die Gerade line1 durch die zwei Punkte [-3,1] and [3,-1] erzeugt. Für jeden der beiden Punkte haben wir $x$- und $y$-Koordinate in der Form [x, y] angegeben. Da wir für die Gerade eine Liste mit zwei Punkten benötigen, sind beide Koordinatenpaare wiederum in eckige Klammern eingeschlossen. Kurz gesagt, die Liste der Koordinaten der beiden Punkte wird mit [[-3,1],[3,-1]] angegeben.

Für die zweite Gerade line2 legen wir zuerst zwei Punkte $p$ und $q$ an und verwenden sie mittels [p,q] um die Gerade line2 festzulegen. Hier sehen wir bereits, warum es nützlich ist, Objekte in Variablen abzuspeichern. Wir könnten nun zum Beispiel eine dritte Gerade anlegen, die ebenfalls durch $p$ und $q$ verläuft, ohne uns sorgen zu müssen, ob die Koordinaten korrekt sind.

Beachte: In Javascript werden Listen mittel eckiger Klammern [ ] angegeben. {/lang}

{lang=EN}

Adding attributes to the objects

Objects in JSXGraph have attributes, which describe them. Some of them are common (like color, name, etc.) and some are more specific. Points have properties for e.g. shape, where lines have other attributes like size, fullness, type of beginning and ending, etc. (more here). We can always look at the JSXGraph API documentation, which describes all the objects and their attributes.

Let us look now at the example. {/lang}

{lang=SI}

Dodajanje atributov k objektom

Objekti v JSXGraphu lahko imajo atribute, ki jih opisujejo. Nekateri so pogosti (npr. barva, ime, velikost), drugi bolj specifični. Različni objekti imajo lahko različne atribute. Vedno si lahko pomagamo z JSXGraph API dokumentacijo, ki opisuje vse objekte in vse njihove atribute.

Poglejmo primer. {/lang}

{lang=CZ}

Nastavení vlastností objektů

Objekty v JSXGraphu mají atributy, které je charakterizují. Některé z nich jsou společné všem (jako barva, jméno apod.), některé jsou typické pro objekty konkrétního druhu. Body mají například různé tvary, u přímky pak lze např. stanovit, zda bude končit v druhém ze svých určujících bodů (atribut straightLast) a jak v něm bude končit (více zde).

Popisy všech atributů objektů JSXGraphu jsou uvedeny v dokumentaci JSXGraph Reference.

Podívejme se na následující příklad: {/lang}

{lang=DE}

Attribute zu Objekten hinzufügen

JSXGraph-Objekte besitzen Attribute, durch die sie beschrieben werden. Einige dieser Attribute stehen in allen Objekte zur Verfügung (z.B. color, name, etc.), andere Attribute gibt es nur bei speziellen Objekten. Zum Beispiel besitzen Punkte das Attribut shape, Geraden dagegen besitzen u.a. Attribute, die festlegen, ob die Gerade über die definierenden Punkte hinausgezeichnet wird oder nicht (Attribute straightFirstund straightLast). Siehe hierzu auch die Dokumentation zu Geraden.

In der umfangreichen JSXGraph API Dokumentation werden alle Objekte und ihre Attribute detailliert beschrieben.

Betrachten wir folgendes Beispiel. {/lang}

<div id="jxgbox" class="jxgbox" style="width:500px; height:200px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-5, 2, 5, -2]});

 var p = board.create('point',[-2,-1],{name:"first", size:5, color:"FF0000"});
 var q = board.create('point',[3,1],{name:"last",fixed:true, face:"[]"});

 var line2 = board.create("line",[p,q],{straightLast:false, dash:"4" });
</script>

{lang=EN} Result: {/lang}

{lang=SI} Rezultat: {/lang}

{lang=CZ} Výsledek: {/lang}

{lang=DE} Resultat: {/lang}

{lang=EN} In this example we added some attributes to both the points and to the line. In all three examples we defined attributes as a list written between { }. For each attribute we must write its name and a value. As we mentioned earlier, objects can have specific attributes and also more general borrowed (inherited) from other objects.

In var p = board.create('point',[-2,-1],{name:"first", size:5, color:"FF0000"}); the first attribute is name which is borrowed from GeometryElement, attribute color is also borrowed, where attribute size is not borrowed but belongs to object Point. We can read from the documentation: Size of a point, either in pixel or user coordinates. It means the radius resp. half the width of a point (depending on the face).

Second point has some interesting attributes var q = board.create('point',[3,1],{name:"last",fixed:true, face:"[]"}); First is the attribute fixed which defines whether objects can be moved (dragged) on the board. the default value for this attribute is false, which means we can move all objects on the board if they are not explicitly fixed. Now we first mentioned default value, which is used when do not explicitly set another value for some attribute. In the documentation for each attribute default value is also presented. The second new attribute is face where we used one of the possible shapes of a point.

When we defined var line2 = board.create("line",[p,q],{straightLast:false, dash:"4" });, we used two attributes, first defining how line will end at second point (straightLast) and second defining how the line will be drawn (dash). Again, dash can have different values, documentation for dash attribute tells us which are possible values.

All objects have attributes, that includes the Board object. One of the attributes is boundingbox, which we used from first example, but didn't talk about until now. E.g. if you don't like the navigation (bottom right), then you can add attribute showNavigation and set it to false. Try it!

We can see that we can use attributes to fine tune how our construction will behave and look.

Documentation is a great resource for discovering attributes and also has some examples of their usage. {/lang}

{lang=SI} V primeru smo dodali nekaj atributov k točkama in premici. V vseh situacijah smo morali atribute našteti med oklepaje { }. Za vsak atribut je potrebno zapisati njegovo ime in vednost. Kot smo že povedali imajo lahko objekti specifične atribute, lahko pa imajo sposojene (podedovane) od drugih objektov.

V vrstici var p = board.create('point',[-2,-1],{name:"first", size:5, color:"FF0000"}); je prvi atribut name, ki je sposojen iz GeometryElement. Atribut color je tudi sposojen, med tem ko size pripada objektu Point.

Za drugo točko uporabimo nekaj zanimivih lastnosti var q = board.create('point',[3,1],{name:"last",fixed:true, face:"[]"}); Prvi atribut je fixed, ki pove, če lahko objekt premikamo po risalni površini. Če tega atributa ne zapišemo sami, je vedno privzeta vrednost false, torej lahko objekt premikamo. Privzeta vrednost je vrednost, ki jo atribut zavzame, če ga sami ne zapišemo. V dokumentaciji objektov so zapisane tudi vse privzete vrednosti atributov. Naslednja nova lastnost je face, s katero določimo obliko objekta.

Pri definicij premice var line2 = board.create("line",[p,q],{straightLast:false, dash:"4" });, smo uporabili dva atributa. Prvi nam pove, na kak način se zaključi črta pri drugi točki (straightLast), drugi pa nam pove, kako bo črta narisana (dash). Ta atribut ima spet lahko več vrednosti, kar si lahko pogledamo v dokumentaciji za dash .

Vsi objekti imajo atribute, tudi objekt Board. Eden izmed teh je boundingbox, ki smo ga uporabili v prvem primeru. Če ne želimo imeti navigacije v spodnjem desnem kotu platna, lahko to storimo z atributom showNavigation, ki mu določimo vrednost false.

Dokumentacija je odličen vir za preučevanje atributov in njihovih vrednosti, ki nam pokaže tudi kakšen primer njihove uporabe. {/lang}

{lang=CZ} V tomto příkladu jsme přidali některé atributy jak k bodům, tak i k přímce. Ve všech třech případech jsme definovali vlastnosti objektů pomocí seznamu atributů uvedených v závorkách { }. Pro každý atribut musíme napsat jeho jméno a hodnotu. Jak již bylo uvedeno dříve, objekty mohou mít jak specifické atributy, tak i atributy obecné, sdílené s více objekty.

V kódu var p = board.create('point',[-2,-1],{name:"first", size:5, color:"FF0000"}); je prvním atributem jméno objektu name, které je společné třídě GeometryElement, atribut barvy color je také společný, zatímco atribut velikosti size není obecný, ale je typický pro objekt Point (bod). V dokumentaci se dočteme: Velikost bodu, buď v pixelech nebo v jednotkách určených uživatelem. Znamená poloměr nebo polovinu šířky bodu (v závislosti na jeho vzhledu).

Kód var q = board.create('point',[3,1],{name:"last",fixed:true, face:"[]"}); definující druhý bod obsahuje další zajímavé atributy. První z nich je atribut fixed, který určuje, zda může být objekt přemisťován (tažen) po nákresně. Nastavená (Default) hodnota pro tento atribut je false, což znamená, že pokud objekty nejsou explicitně fixovány, můžeme s nimi hýbat po nákresně. Nastavená hodnota (default value) je použita vždy, když není pro daný atribut explicitně zadána jiná hodnota. V dokumentaci jsou uvedeny nastavené hodnoty pro všechny atributy. Druhým novým atributem v uvedeném kódu je face, kterým nastavíme jeden z možných tvarů bodu.

V kódu var line2 = board.create("line",[p,q],{straightLast:false, dash:"4" }); definice přímky byly použity dva atributy, první z nich straightLast určuje, že přímka skončí ve druhém z určujících bodů, druhý dash potom určuje, jak bude čára nakreslena. Parametr dash může nabývat různých hodnot, jejich přehled viz dokumentace pro atribut "dash".

Tak jako všechny objekty i nákresna (Board) má své atributy. Jedním z nich je boundingbox, který používáme již od první ukázky kódu nákresny, ale ještě jsme ho nekomentovali. Dalším atributem nákresny je showNavigation, který nám dovoluje skrýt navigační tlačítka v pravém dolním rohu nákresny, pokud mu nastavíme hodnotu false. Vyzkoušejte to!

Vidíme, že pomocí nastavení hodnot atributů můžeme vyladit chování i vzhled naší konstrukce.

Dokumentace je velkým zdrojem pro poznání všech atributů, které můžeme použít. Obsahuje také konkrétní příklady jejich použití. {/lang}

{lang=DE} In diesem Beispiel werden verschiedene Attribute zu den beiden Punkten und der Geraden hinzugefügt. In allen drei Beispielen legen wir die Attribute durch eine Liste, die durch geschweifte Klammern { } eingeschlossen ist, fest. Für jedes Attribut wird sein Name und ein Wert angegeben. Wie bereits erwähnt, haben Objekte sowohl spezifische Attribute als auch allgemeinere Objekte, die von anderen Objekten vererbt sind.

In var p = board.create('point',[-2,-1],{name:"first", size:5, color:"FF0000"}); ist das erste Attribut name, das vom Element GeometryElement abgeleitet ist. Das Attribut color ist ebenfalls von diesem Element abgeleitet und daher in nahezu allen Elementen verfügbar. Das Attribut size hingegen ist ausschließlich im Objekt Punkt verfügbar.

Aus der Dokumentation zum Attribute size: Size of a point, either in pixel or user coordinates. Means radius resp. half the width of a point (depending on the face).

Dem zweiten Punkt im obigen Beispiel werden die interessanten Attribute var q = board.create('point',[3,1],{name:"last",fixed:true, face:"[]"}); zugewiesen. Das Attribut fixed legt fest, ob das Objekt vom Betrachter bewegt (gezogen) werden kann. Der Standardwert für dieses Attribut ist false, was heißt, dass wir alle Objekte über die Zeichenfläche ziehen können, für die dies nicht explizit mit fixed:true unterbunden ist.

Wir habe gerade erstmals den Standardwert (default value) eines Attributs erwähnt. Dieser wird verwendet, wenn nicht explizit ein anderer Wert gesetzt wird. In der Dokumentation wird für jedes Attribut der zugehörige default value aufgelistet.

Das zweite neue Attribut ist face, mit dem wir eine der möglichen Punktformen gewählt hatten.

Bei der Angabe var line2 = board.create("line",[p,q],{straightLast:false, dash:"4" }); setzen wir zwei Attribute. Mit dem ersten Attribut wird bestimmt, dass die "Gerade" am zweiten Punkt endet (straightLast). Also wird eine Halbgerade zu sehen sein. Das zweite Attribut legt die Linienform der Geraden fest (dash): durchgezogen, gestrichelt, etc. Wie zuvor kann dash verschiedene Werte annehmen, in der Dokumentation für das dash-Attribut sind die möglichen Werte aufgelistet.

Alle Objekte haben Attribute, auch das board-Objekt hat Attribute. Eines dieser Attribute ist boundingbox, das bereits im ersten Beispiel verwendet wurde, aber über das noch nichts weiter gesagt wurde.

Wenn zum Beispiel die Navigations-Icons unten rechts ausgeblendet werden sollen, so kann das Board-Attribut showNavigation auf false gesetzt werden. Versuchen wir es!

Wir sehen, dass wir mit Attributen Feineinstellungen zum Verhalten und Aussehen unserer Konstruktion vornehmen können.

Die Dokumentation ist eine hervorragende Quelle um Attribute zu entdecken. Zudem enthält sie viele Beispiele, wie Attribute verwendet werden. {/lang}

{lang=EN}

Example

Harmonic conjugate points. Given three collinear points A, B and C; C being outside the line segment AB. Determine the point D of the segment AB so that the ratio of its distances to A and B, respectively, is equal to the ratio of distances of the point C to points A and B, respectively, i.e. |AD|/|BD|=|AC|/|BC|.

This point D is called the harmonic conjugate of C with respect to A and B and points A, B, C and D together form the so called harmonic quadruple. {/lang}

{lang=CZ}

Příklad

Harmonická čtveřice bodů. Jsou dány tři kolineární body A, B a C; C leží vně úsečky AB. Určete bod D úsečky AB takový, že poměr jeho vzdáleností od bodů A a B, v daném pořadí, je roven poměru vzdáleností bodu C od bodů A a B, tj. |AD|/|BD|=|AC|/|BC|.

Bod D potom nazýváme harmonicky sdružený s bodem C vzhledem k bodům A a B, takové body A, B, C a D potom společně vytváří tzv. harmonickou čtveřici. {/lang}

{lang=SI}

Primer

Harmonično konjugirane točke. Naj bodo podane tri kolinearne točke A, B in C, kjer se C nahaja izven daljice AB. Določimo točko D na daljici AB tako, da velja razmerje |AD|:|BD|=|AC|:|BC|.

Točko D imenujemo harmonična konjugiranka točke C glede na A in B. Točke A, B, C in D skupaj tvorijo harmonično štirico. {/lang}

{lang=DE}

Beispiel

Harmonische Teilung. Gegeben sind drei kollineare Punkte A, B und C (d.h. sie liegen auf einer Geraden), wobei C ausserhalb der Strecke AB liege. Bestimme einen Punkt D auf der Strecke AB so, dass das Verhältnis seiner Abstände zu den Punkten A und B jeweils gleich dem Verhältnis der Abstände des Punktes C zu den Punkten A bzw. B ist, das heißt |AD|/|BD|=|AC|/|BC|.

Diese Konstellation wird harmonische Teilung genannt. {/lang}

{lang=EN} Result: To solve the task, we construct the so called complete quadrangle, as shown below. {/lang}

{lang=CZ} Výsledek: K řešení úlohy využijeme konstrukci tzv. úplného čtyřrohu, jak vidíme níže. {/lang}

{lang=SI} Rezultat: Da rešimo problem, najprej konstruiramo tako imenovani popolni štirikotnik, kot je prikazano spodaj. {/lang}

{lang=DE} Resultat: Zur Lösung der Aufgabe konstruieren wir das sogenannte vollständige Viereck, wie unten zu sehen ist. {/lang}

{lang=EN} Programming:

First, we define the bounding box and create two points A and B with the line p passing through them: {/lang}

{lang=CZ} Programování:

Nejprve definujeme parametry nákresny, tj. rozměry okna a rozsah souřadnic, a v ní sestrojíme body A a B spolu s přímkou p, která jimi prochází: {/lang}

{lang=SI} Programiranje:

Najprej definiramo bounding box in ustvarimo točki A in B z premico p, ki poteka skozi njiju. {/lang}

{lang=DE} Programmierung:

Zuerst legen wir die bounding box fest und erzeugen zwei Punkte A und B sowie die Gerade p durch die beiden Punkte: {/lang}

<div id="jxgbox" class="jxgbox" style="width:500px; height:400px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-5, 5, 5, -3]});
 var A = board.create('point',[-4,-2]);
 var B = board.create('point',[0,-2]);
 var p = board.create('line',[A,B],{name: 'p',withLabel: true, color: 'green'});
</script>

{lang=EN} Then, we put the point C on p so that it can move along it: {/lang}

{lang=CZ} Potom na přímku p umístíme bod C tak, aby byl po ní volně pohyblivý: {/lang}

{lang=SI} Potem postavimo točko C na premico p tako, da se lahko premika samo vzdolž nje. {/lang}

{lang=DE} Dann legen wir den Punkt C auf die Gerade p, so dass wir ihn nur entlang der Geraden ziehen können. $C$ wird glider genannt. {/lang}

<div id="jxgbox" class="jxgbox" style="width:500px; height:400px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-5, 5, 5, -3]});
 var A = board.create('point',[-4,-2]);
 var B = board.create('point',[0,-2]);
 var p = board.create('line',[A,B],{name: 'p',withLabel: true, color: 'green'});
 var C = board.create('glider', [4, 0, p]);
</script>

{lang=EN} Now, we put the fourth point E above the line p and connect it by the straight lines q and r to points A and B, respectively: {/lang}

{lang=CZ} Nyní umístíme čtvrtý bod E nad přímku p a přímkami q a r ho spojíme v daném pořadí postupně s body A a B: {/lang}

{lang=SI} Nato postavimo četrto točko E nad premico p in jo povežemo z črtama q in r do točk A in B. {/lang}

{lang=DE} Nun erzeugen wir einen vierten Punkt E oberhalb der Geraden p an und konstruieren zwei Geraden q und r durch A bzw. B: {/lang}

<div id="jxgbox" class="jxgbox" style="width:500px; height:400px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-5, 5, 5, -3]});
 var A = board.create('point',[-4,-2]);
 var B = board.create('point',[0,-2]);
 var p = board.create('line',[A,B],{name: 'p',withLabel: true, color: 'green'});
 var C = board.create('glider', [4, 0, p]);
 var E = board.create('point', [1,4], {name: 'E',size:2, color: 'blue'});
 var q = board.create('line',[A,E],{name: 'q',withLabel: true, color: 'green'});
 var r = board.create('line',[B,E],{name: 'r',withLabel: true, color: 'green'});
</script>

{lang=EN} After this, we put the point F on q, somewhere between A and E, draw a line s passing through points C and F and determine its intersection G with the line r: {/lang}

{lang=CZ} Poté umístíme na přímku q bod F, někam mezi body A a E, sestrojíme přímku s procházející body C a F a určíme její průsečík G s přímkou r: {/lang}

{lang=SI} Za tem določimo točko F na premici q nekje med A in E, narišemo premico s skozi točki C in F in določimo njeno presečišče s premico r. {/lang}

{lang=DE} Danach legen wir einen Punkt F auf die Gerade q (d.h. einen glider) irgendwo zwischen A und E, ziehen eine Gerade s durch C und F und bestimmen ihren den Schnittpunkt G mit der Geraden r: {/lang}

<div id="jxgbox" class="jxgbox" style="width:500px; height:400px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-5, 5, 5, -3]});
 var A = board.create('point',[-4,-2]);
 var B = board.create('point',[0,-2]);
 var p = board.create('line',[A,B],{name: 'p',withLabel: true, color: 'green'});
 var C = board.create('glider', [4, 0, p]);
 var E = board.create('point', [1,4], {name: 'E',size:2, color: 'blue'});
 var q = board.create('line',[A,E],{name: 'q',withLabel: true, color: 'green'});
 var r = board.create('line',[B,E],{name: 'r',withLabel: true, color: 'green'});
 var F = board.create('glider', [0,0,q], {name: 'F',size:2, color: 'blue'});
 var s = board.create('line',[C,F],{name: 's',withLabel: true, color: 'green'});
 var G = board.create('intersection', [s, r,0], {name: 'G',size:2, color: 'blue'});
</script>

{lang=EN} Finally, we draw lines t=AG and u=BF, denote H their point of intersection, construct the line v passing points H and E and determine the desired point D as the intersection of lines v and p: {/lang}

{lang=CZ} Nakonec sestrojíme přímky t=AG a u=BF, určíme a označíme H jejich průsečík, sestrojíme přímku v procházející body H a E a určíme hledaný bod D jako průsečík přímek v a p: {/lang}

{lang=SI} Na koncu narišemo črti t=AG in u=BF, s H označimo njuni presečišči, konstruiramo premico v skozi h in E ter s črko D označimo presečišče premic v in p. {/lang}

{lang=DE} Schließlich, erzeugen wir die Geraden t=AG und u=BF, bezeichnen mit H ihren Schnittpunkt, konstruieren die Gerade v durch die Punkte H und E und bestimmen den gewünschten Punkt D als den Schnittpunkt der Geraden v und p: {/lang}

<div id="jxgbox" class="jxgbox" style="width:500px; height:400px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-5, 5, 5, -3]});
 var A = board.create('point',[-4,-2]);
 var B = board.create('point',[0,-2]);
 var p = board.create('line',[A,B],{name: 'p',withLabel: true, color: 'green'});
 var C = board.create('glider', [4, 0, p]);
 var E = board.create('point', [1,4], {name: 'E',size:2, color: 'blue'});
 var q = board.create('line',[A,E],{name: 'q',withLabel: true, color: 'green'});
 var r = board.create('line',[B,E],{name: 'r',withLabel: true, color: 'green'});
 var F = board.create('glider', [0,0,q], {name: 'F',size:2, color: 'blue'});
 var s = board.create('line',[C,F],{name: 's',withLabel: true, color: 'green'});
 var G = board.create('intersection', [s, r,0], {name: 'G',size:2, color: 'blue'});
 var t = board.create('line',[A,G],{color: 'grey', dash:"2"});
 var u = board.create('line',[B,F],{color: 'grey', dash:"2"});
 var H = board.create('intersection', [t, u], {name: 'H',size:2, color: 'blue'});
 var v = board.create('line', [E,H],{color: 'grey', dash:"2"});
 var D = board.create('intersection', [p, v, 0]);
</script>

{lang=EN}

Circles

In JSXGraph we don't have only points and lines. In this section we will learn about circles. They can be constructed with different methods, here we will present how to create a circle with either two points, or a point and a radius. Let us look at the example. {/lang}

{lang=SI}

Krogi

V JSXGraphu nimamo samo točk in premic. V tem poglavju se bomo naučili konstruirati krožnice in kroge. Uporabimo lahko različne metode. Pokazali bomo, kako definirati krog bodisi z dvema točkama, bodisi s točko in polmerom. {/lang}

{lang=CZ}

Kružnice

V JSXGraphu nemáme k dispozici jenom body a přímky. Jsou zde definovány ještě další objekty, se kterými se postupně seznámíme. Tato kapitola pojednává o kružnicích. Ty mohou být sestrojeny různými metodami. Zaměříme se na dvě z nich, konstrukci kružnice dané dvěma body a konstrukci kružnice dané bodem a poloměrem. Podívejme se na následující příklad: {/lang}

{lang=DE}

Kreise

In JSXGraph haben wir nicht nur Punkte und Geraden zur Verfügung. In diesem Kapitel lernen wir Kreise kennen. Sie können auf mehrere verschiedene Weisen konstruiert werden. Hier zeigen wir die Konstruktionen durch zwei Punkte, sowie durch einen Punkt und einen Radius. Betrachten wir ein Beispiel: {/lang}

<div id="jxgbox" class="jxgbox" style="width:500px; height:200px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-5, 2, 5, -2],
     keepAspectRatio:true});

 var p = board.create('point',[-1,-1],{name:"A"});
 var q = board.create('point',[0,0],{name:"B"});

 var circle1 = board.create("circle",[p,q],{strokeColor:"red", strokeWidth:4});
 var circle2 = board.create("circle",["B",1.8],{method:"pointRadius", fillColor:"gray",
     fillOpacity:0.2});
</script>

{lang=EN} The first thing what we notice is, that we initialized the board with a new argument keepAspectRatio:true which we use to tell JSXGraph that we want our drawing board to keep the aspect ratio between the $x$ and $y$ axis. Setting this to true is necessary if circles should look like circles and not like ellipses.

After creating both points we create two circles. Circle1 is created with var circle1 = board.create("circle",[p,q],{strokecolor:"red", strokeWidth:4});. We can see that here we created circle with two points which is default method for creating the circles. We used two additional attributes which we used to set the color and width of the stroke. Color here was not defined with RGB system, but with the color name.

Circle2 is more interesting var circle2 = board.create("circle",["B",1.8],{method:"pointRadius", fillcolor:"gray", fillopacity:0.2}); since we created it with the point and radius method. We explicitly set this as a attribute. Also instead of using variable name for the point, we used name of the point "B", which can be very useful when having many objects in the construction (and generating objects dynamically). We also used two attributes for filling the area of circle, namely fillColor which defines the color of the fill and fillOpacity sets the opacity of the area (ranging from $0$ to $1$, where $1$ means solid color with no opacity). {/lang}

{lang=SI} Najprej opazimo, da smo risalno desko opremili z novim atributom, to je keepAspectRatio:true, s katerim povemo, da želimo ohraniti razmerje med osjo $x$ in $y$. Vrednost moramo nastaviti na true, če želimo, da naši krogi izgledajo kot krogi in ne kot elipse.

Ko ustvarimo obe točki lahko definiramo kroga. Circle1 konstruiramo z var circle1 = board.create("circle",[p,q],{strokecolor:"red", strokeWidth:4});. Narisali smo torej krog, ki gre skozi točki $p$ in $q$. Uporabili smo tudi dva atributa, s katerima smo določili barvo in debelino črte. Pri tem nismo barve definirali z RGB sistemom, ampak z imenom barve.

Drugi krog Circle2 je bolj zanimiv: var circle2 = board.create("circle",["B",1.8],{method:"pointRadius", fillcolor:"gray", fillopacity:0.2});, ker smo ga ustvarili z metodo točke in polmera, kar moramo posebej sporočiti kot atribut method:"pointRadius". Pri tem nismo uporabili imena spremenljivke točke, ampak njeno ime B, kar je tudi veljaven način za sklicevanje na že prej zapisane objekte. Zapisali smo tudi dva nova atributa za zapolnitev notranjosti kroga, torej fillColor in fillOpacity, ki določita barvo in motnost notranjosti. {/lang}

{lang=CZ} Především je třeba zmínit, že jsme v příkazu pro inicializaci nákresny použili nový atribut keepAspectRatio:true, kterým dáváme JSXGraphu pokyn, aby byl zachován poměr stran nákresny odpovídající rozsahům hodnot na osách $x$ a $y$. Nastavení hodnoty true je nezbytné pro to, aby kružnice vypadaly v nákresně skutečně jako kružnice a ne jako elipsy.

Nyní k vlastní konstrukci kružnice. Kružnice Circle1 je definována kódem var circle1 = board.create("circle",[p,q],{strokecolor:"red", strokeWidth:4});, kde p, q jsou dva body, které jí určují, p je střed kružnice a q je bod, kterým kružnice prochází. V definici jsou užity dva atributy pro barvu a tloušťku čáry. Barva přitom není definována systémem RGB, ale jménem barvy.

Kružnice Circle2 je zajímavější, protože je dána středem a poloměrem. Definujeme ji kódem var circle2 = board.create("circle",["B",1.5],{method:"pointRadius", fillcolor:"gray", fillopacity:0.2}); Tato metoda konstrukce kružnice musí být zadána explicitně formou atributu, na rozdíl od té předchozí, která je v JSXGraphu implicitní. Také stojí za povšimnutí, že jsme v tomto kódu nepoužili jméno proměnné q, do které je bod uložen, ale přímo jméno "B" tohoto bodu. Což může být velmi užitečné, když máme v konstrukci více objektů a když jsou objekty generovány dynamicky.

Použili jsme dva atributy pro vyplnění vnitřku kružnice (vytvoření kruhu), konkrétně fillColor, který definuje barvu výplně a fillOpacity, kterým nastavíme neprůhlednost této plochy (kruhu) (nabývá hodnot od $0$ do $1$, kde $1$ znamená jednobarevnou výplň bez průhlednosti). {/lang}

{lang=DE} Zuerst sehen wir, dass bei der Initialisierung der Zeichenfläche das neue Attribut keepAspectRatio:true verwendet wurde, um JSXGraph mitzuteilen, dass wir das Verhältnis zwischen $x$- und $y$-Achse im HTML-Objekt gleich haben wollen. Dies ist notwendig, damit Kreise wie Kreise aussehen und nicht wie Ellipsen, falls das Verhältnis von Breite zu Höhe des HTML-Objektes nicht dem Verhältnis von Breite zu Höhe der bounding box entspricht.

Nach dem Anlegen zweier Punkte konstruieren wir zwei Kreise. circle1 wird erzeugt durch var circle1 = board.create("circle",[p,q],{strokecolor:"red", strokeWidth:4});. Wir sehen, dass hier ein Kreis durch Angabe zweier Punkte erzeugt wird. Dies ist wahrscheinlich die Standardmethode zur Kreiserzeugung. Dabei verwenden wir zwei weitere Attribute mit denen wir die Farbe und Breite der Kreislinie setzen. Die Farbe wird in diesem Fall nicht im RGB-System angegeben, sondern durch einen Farbnamen.

circle2 ist noch interessanter:

var circle2 = board.create("circle",["B",1.8],{method:"pointRadius", fillcolor:"gray", fillopacity:0.2});

Dieser Kreis wird mit der Punkt-Radius-Methode erzeugt. Wir geben diese Methode explizit als Attribut an. Das ist zwar nicht unbedingt nötig, aber sicher ist sicher. Zudem - anstatt für den Mittelpunkt einen Variablennamen oder ein Koordinatenpaar anzugeben - verwenden wir den Namen des Punktes "B", was sehr nützlich sein kann, falls die Konstruktion sehr viele Objekte enthält (und Objekte dynamisch erzeugt werden). Ausserdem verwenden wir zwei Attribute zur Färbung der Kreisfläche: fillColor legt die Füllfarbe fest und fillOpacity setzt die Durchsichtigkeit (Opacity) der Kreisfläche und nimmt Werte zwischen $0$ und $1$ an, wobei $1$ undurchsichtig bedeutet. {/lang}

{lang=EN}

Polygons

Polygons are very useful objects which can be used to construct a closed area with arbitrarily many points (minimum is three). Polygons can be convex or concave, depending on the input points. We can again define different attributes to the object.

Example: {/lang}

{lang=SI}

Poligoni

Poligoni ali n-kotniki so objekti, s katerimi rišemo zaprta območja omejena s poljubno mnogo točkami (najmanj tremi). Lahko so konveksni ali konkavni, odvisno od podanih točk. Spet lahko definiramo različne atribute. Poglejmo primer: {/lang}

{lang=CZ}

Mnohoúhelníky

Mnohoúhelníky jsou v geometrii velmi frekventované objekty. Můžeme je chápat jako části roviny ohraničené uzavřenou lomenou čarou s libovolným počtem vrcholů (minimum jsou tři). Mnohoúhelník může být konvexní nebo konkávní (říkáme též nekonvexní), v závislosti na rozložení určujících bodů (vrcholů). Stejně jako jiným objektům i mnohoúhelníkům můžeme přiřadit různé atributy.

Příklad: {/lang}

{lang=DE}

Polgyone

Polygone (Vielecke) sind sehr hilfreiche Objekte zur Konstruktion von abgeschlossenen Flächen (Vielecke) mit beliebig vielen Eckpunkten (aber minimal drei). Polygone können konvex sein, müssen es aber nicht. Dies ist abhängig von den definierenden Punkten. Auch hier können wir mit verschiedenen Attributen das Aussehen und Verhalten ändern.

Beispiel: {/lang}

<div id="jxgbox" class="jxgbox" style="width:500px; height:200px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-5, 2, 5, -2],
     keepAspectRatio:true, showCopyright:false, showNavigation:false });

 var p = board.create('point',[-2,0],{name:"A"});
 var q = board.create('point',[-1,-1],{name:"B"});
 var r = board.create('point',[1,-0.5],{name:"C"});
 var s = board.create('point',[1,1],{name:"D"});
 var t = board.create('point',[-1,1.5],{name:"E"});

 var poly1 = board.create('polygon',[p,q,r,s,t],{name:"Polygon 1",withLabel:true});

 var points = [[2,-1],[4,1],[1,1],[-1,-1]];
 var poly2 = board.create('polygon',points,{name:"Polygon 2",withLabel:true,
     hasInnerPoints:true, withLines:false, vertices:{visible:false}});
</script>

{lang=EN} As we mentioned earlier we need at least three points to make a polygon. In our example we created five points which were then used to create a polygon. We used an attribute withLabel which tells JSXGraph to show the name of the polygon.

For the second polygon we created a list of points, which is another approach to creating a polygon. Here we have a few new attributes. Attribute hasInnerPoints enables the user to move the entire polygon. For example, moving Polygon 1 is not possible, only its points can be moved. Adding this attribute will enable moving the polygon. Next attribute, withLines tells JSXGraph whether to draw borders of the polygon or not. The last attribute vertices is particularly interesting, because it does not have just a value, but a dictionary on the right side of :. The reason behind it is that we can control the vertices with more than one attribute. {/lang}

{lang=SI} Kot smo že omenili, potrebujemo za definicijo poligona vsaj tri točke. V našem primeru smo ustvarili 5 točk in nad njimi definirali poligon. Uporabili smo atribut withLabel, ki pove, da naj bo na sliki označeno ime poligona.

V drugem primeru pa smo ustvarili seznam točk in s pomočjo seznama definirali 4-kotnik. Tukaj imamo ponovno nekaj novih atributov. Atribut hasInnerPoints omogoča uporabniku, da premika celoten objekt. Pri prvem poligonu to ni mogoče, lahko premikamo samo njegove robne točke. Naslednji atribut withLines pove JSXGraphu, da naj nariše robove poligona. Zadnji atribut vertices je posebej zanimiv, saj nima samo vrednosti, ampak ima slovar na desni strani dvopičja. Razlog za to je v tem, da lahko oglišča nadzorujemo z več kot eno lastnostjo. {/lang}

{lang=CZ} Jak je zřejmé z geometrické podstaty mnohoúhelníku, pro jeho vytvoření potřebujeme alespoň tři body. V uvedeném příkladě jsme vytvořili pět bodů, které jsme pojmenovali A, B, C, D, E a použili jsme je k určení prvního mnohoúhelníku, pětiúhelníku ABCDE. V jeho definici jsme použili atribut withLabel s hodnotou true, kterým jsme zajistili zobrazení jména pětiúhelníku Polygon 1.

K určení druhého mnohoúhelníku, tentokrát se jedná o čtyřúhelník, jsme použili předem vytvořenou posloupnost vrcholů, což je další přístup k definování mnohoúhelníku v JSXGraphu. V definici jsme použili několik dalších nových atributů.

Atribut hasInnerPoints přináší možnost pohybovat v nákresně s celým mnohoúhelníkem. Srovnejme s pětiúhelníkem ABCDE (Polygon 1), který nemůžeme celý přemístit, můžeme pohybovat pouze s jeho jednotlivými vrcholy.

Další atribut, withLines je zodpovědný za to, zda se bude (implicitní nastavení, při použití atributu withLines hodnota true) nebo nebude (atribut withLines s hodnotou false) kreslit hranice mnohoúhelníku.

Poslední atribut vertices, který se týká vrcholů mnohoúhelníku, je zajímavý tím, že mu za dvojtečkou : není přiřazena jedna hodnota, ale seznam dalších atributů s jejich hodnotami. Důvodem je skutečnost, že výskyt vrcholů může být ovládán více atributy. {/lang}

{lang=DE} Wie breits erwähnt, benötigen wir mindestens drei Punkte zur Konstruktion eines Polygons. In unserem Beispiel haben wir zuerst fünf Punkte angelegt, die dann unser Polgon definieren werden. Wir haben zusätzlich das Attribut withLabel:true angegeben, um den Namen des Polygons anzuzeigen.

Zur Konstruktion des zweite Polygons verwenden wir eine Liste von Koordinatenpaaren, sowie einige neue Attribute. Das Attribut hasInnerPoints ermöglicht es dem Berachter, das gesamte Polygon zu verschieben. Im Gegensatz dazu kann Polygon 1 nicht komplett verschoben werden, lediglich einzelne Punkte oder Kanten können verzogen werden. Das nächste Attribut withLines teilt JSXGraph mit, ob die Kanten / Ränder des Polygons angezeigt werden sollen oder nicht. Das letzte Attribut vertices ist wieder besonders interessant, denn es besitzt keinen einfachen Wert. Nach dem : folgt ein eigenes Attribut-Objekt, das die Eigenschaften der Polygon-Ecken festlegt. Der Grund ist, dass wir oft mehr als ein Attribut der Ecken verändern wollen. {/lang}

{lang=EN}

Example: Regular polygons

A Hexagon-Triangle Hinge. In the diagram below, Q is the center of a regular hexagon with a vertex B at which it touches an equilateral triangle with center R. Let P be the midpoint of AG. Show that RPQ is a right angle.

(Source: Konhauser, J. D. E., Velleman, D., Wagon, S. Which Way Did the Bicycle Go? … and Other Intriguing Mathematical Mysteries. The Mathematical association of America, Dolciani Mathematical Expositions – No. 18. 1996.) {/lang}

{lang=CZ}

Příklad: Pravidelné mnohoúhelníky

Pravidelný šestiúhelník a rovnostranný trojúhelník se společným vrcholem. Na obrázku níže je bod Q středem pravidelného šestiúhelníku, který svůj vrchol B sdílí s rovnostranným trojúhelníkem, jehož středem je bod R. Středem úsečky AG je bod P. Dokažte, že úhel RPQ je pravý.

(Zdroj: Konhauser, J. D. E., Velleman, D., Wagon, S. Which Way Did the Bicycle Go? … and Other Intriguing Mathematical Mysteries. The Mathematical association of America, Dolciani Mathematical Expositions – No. 18. 1996.) {/lang}

{lang=SI}

Primer: Pravilni n-kotniki

Tečaj iz šestkotnika in trikotnika. V spodnji sliki je Q središče pravilnega 6-kotnika z ogliščem B, v katerem se dotika enakokrakega trikotnika s središčem R. Naj bo P razpolovišče daljice AG. Pokažimo, da je RPQ pravi kot.

(Vir: Konhauser, J. D. E., Velleman, D., Wagon, S. Which Way Did the Bicycle Go? … and Other Intriguing Mathematical Mysteries. The Mathematical association of America, Dolciani Mathematical Expositions – No. 18. 1996.) {/lang}

{lang=DE}

Beispiel: Reguläre Polygone

Ein Sechseck-Dreiecks-Gelenk. In der folgenden Konstruktion sei Q der Mittelpunkt eines regulären Sechsecks, das eine Ecke B besitzt, mit der es ein gleichseitiges Dreieck mit Mittelpunkt R berührt. Zusätzlich sei P der Mittelpunkt der Strecke AG. Zeige, dass RPQ ein rechter Winkel ist.

(Quelle: Konhauser, J. D. E., Velleman, D., Wagon, S. Which Way Did the Bicycle Go? … and Other Intriguing Mathematical Mysteries. The Mathematical association of America, Dolciani Mathematical Expositions – No. 18. 1996.) {/lang}

{lang=CZ} Řešení příkladu, tj. důkaz uvedeného tvrzení, přenecháváme čtenáři. Zde se budeme věnovat pouze programování dynamického obrázku ilustrujícího daný problém. {/lang}

{lang=SI} Rešitve oziroma pisnega dokaza tukaj ne bomo zapisali, ampak bomo samo demonstrirali, kako sprogramirati dinamično skico iz katere je razvidna resničnost trditve. {/lang}

{lang=DE} Die Lösung der Aufgabe, d.h. der Beweis der Behauptung, sei dem Leser überlassen. Hier wollen wir uns nur mit der Programmierung der erläuternden dynamischen Zeichnung widmen. {/lang}

{lang=EN} Programming:

First, we define the Bounding box as follows: {/lang}

{lang=CZ} Programování:

Nejprve musíme definovat parametry nákresny: {/lang}

{lang=SI} Programiranje:

Najprej definiramo bounding box na naslednji način: {/lang}

{lang=DE} Programmierung:

Zuerst geben wir die bounding box wie folgt an: {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:300px;"></div>
<script>
var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-4, 3, 4, -3]});
</script>

{lang=EN} There will be eleven points in the diagram, namely vertices of polygons, their centers and a midpoint. To set their appearance we use two general options, as follows. First, to get the best possible positions of their labels, with as few overlaps with image lines as possible, we use the autoPosition = true option (it works in v1.1+): {/lang}

{lang=CZ} Obrázek obsahuje celkem jedenáct bodů spolu s jejich popisky, konkrétně se jedná o vrcholy mnohoúhelníků, jejich středy a střed úsečky AG. Pro nastavení jejich zobrazení použijeme následující dvě obecné volby. Jednak, pro co nejlepší zobrazení popisků bodů, s minimem překryvů s čarami obrázku, použijeme volbu autoPosition = true (dostupná ve verzi v1.1+): {/lang}

{lang=SI} Na skici bo prisotnih 11 točk, ki bodo predstavljale oglišča, presečišča in središča likov. Da bo slika izgledala čim bolj berljivo, nastavimo dve lastnosti. Lastnost autoPosition = true bo narisala imena točk na ta način, da bo čim manj prekrivanja. {/lang}

{lang=DE} In der Zeichnung sind elf Punkte enthalten, nämlich die Ecken der Polygone, deren Mittelpunke und ein Strecken-Mittelpunkt. Um ihr Aussehen festzulegen, setzen wir zwei Attribute für alle Elemente der Konstruktion. Wir setzen autoPosition = true. Damit wird das Überlappen von Beschriftungen und Strecken möglichst zu verhindert (ab Version 1.1.0). {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:300px;"></div>
<script>
var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-4, 3, 4, -3]});
			board.options.label.autoPosition = true;
</script>

{lang=EN} Then, we set the basic point size to 1: {/lang}

{lang=CZ} Jednak nastavíme základní velikost bodů na 1: {/lang}

{lang=SI} Nato nastavimo osnovno velikost vseh točk na 1: {/lang}

{lang=DE} Ausserdem setzen wir die Standardgröße der Punkte auf den Wert 1: {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:300px;"></div>
<script>
var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-4, 3, 4, -3]});
			board.options.label.autoPosition = true;
			board.options.point.size = 1;
</script>

{lang=EN} Note: In this way we can also set other common attributes of objects in the board, for example the appearance of points using the command board.options.point.face = '[]'; etc. {/lang}

{lang=CZ} Poznámka: Tímto způsebem můžeme nastavit další společné atributy objektů v nákresně, např. podobu symbolu bodu použitím příkazu board.options.point.face = '[]'; atd. {/lang}

{lang=SI} Opomba: Na ta način lahko poenotimo tudi ostale atribute enakih objektov, naprimer izgled točk z ukazom board.options.point.face = '[]'; ipd. {/lang}

{lang=DE} Hinweis: Auf diese Weise können auch andere Attribute für die gesamte Konstruktion vorbelegt werden, zum Beispiel das Erscheinungsbild von Punkten mit dem Befehl board.options.point.face = '[]'; etc. {/lang}

{lang=EN} To obtain the regular hexagon we first construct points A and B, its future two adjacent vertices, and then color them orange to highlight them as movers:
{/lang}

{lang=CZ} Pro konstrukci pravidelného šestiúhelníku nejprve sestrojíme body A a B, jeho budoucí sousedící vrcholy, a obarvíme je oranžově, pro zdůraznění toho, že se jedná o volné body: {/lang}

{lang=SI} Za konstrukcijo pravilnega 6-kotnika najprej ustvarimo točki A in B in ju pobarvamo oranžno, da ju označimo kot točki, ki ju je možno premikati: {/lang}

{lang=DE} Um ein reguläres Sechseck anzulegen, konstruieren wir zuerst die Punkte A und B als zwei nebeneinanderliegende Ecken des künftigen Sechsecks und färben diese orange um sie als beweglich / ziehbar zu markieren: {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:300px;"></div>
<script>
var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-4, 3, 4, -3]});
			board.options.label.autoPosition = true;
			board.options.point.size = 1;
var A = board.create('point' , [-1.2,-2], {color:  'orange' , size: 4 });
var B = board.create('point',  [0.25,-0.5], {color:  'orange' , size: 4 });
</script>

{lang=EN} Then, using these points as the input parameters to the regularpolygon object, we create the desired hexagon:
{/lang}

{lang=CZ} Poté použijeme tyto body jako vstupní parametry objektu regularpolygon pro vytvoření požadovaného šestiúhelníku: {/lang}

{lang=SI} Nato uporabimo ti točki kot vhodna parametra za konstrukcijo objekta pravilni n-kotnik: {/lang}

{lang=DE} Wir verwenden nun diese Punkte als Eingabeparameter für das regularpolygon-Objekt, um das gewünschte reguläre Sechseck anzulegen:
{/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:300px;"></div>
<script>
var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-4, 3, 4, -3]});
			board.options.label.autoPosition = true;
			board.options.point.size = 1;
var A = board.create('point' , [-1.2,-2], {color:  'orange' , size: 4 });
var B = board.create('point',  [0.25,-0.5], {color:  'orange' , size: 4 });
var hexagon = board.create('regularpolygon', [A,B, 6]);
</script>

{lang=EN} The center of the regular polygon is the center of its circumcircle, therefore we have to identify at least three vertices of the hexagon to determine its center. We chose D, the fourth vertex from A (index number is 3 because the software starts to count from 0)
{/lang}

{lang=CZ} Střed pravidelného šestiúhelníku je zároveň středem jemu opsané kružnice. Pro jeho určení proto potřebujeme identifikovat alespoň tři vrcholy šestiúhelníku. K vrcholům A a B přidáme ještě bod D, v pořadí čtvrtý vrchol od A (protože program začíná indexovat od 0, je indexem tohoto vrcholu číslo 3)
{/lang}

{lang=SI} Središče pravilnega n-kotnika je enako središču njegove očrtane krožnice, zato moramo določiti tri oglišča 6-kotnika. Poleg A in B smo izbrali še oglišče D, to je četrto oglišče od oglišča A (indeks tega oglišča ni 4, ampak 3, saj se štetje seznamov začne pri 0). {/lang}

{lang=DE} Der Mittelpunkt des regulären Polygons ist der Mittelpunkt des Umkreises. Wir müssen daher auf mindestens drei Ecken des Sechsecks zugreifen um seinen Mittelpunkt bestimmen zu können. Wir wählen D, die vierte Ecke von A aus (diese Ecke hat den Index 3, weil die Software bei 0 zu zählen beginnt), {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:300px;"></div>
<script>
var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-4, 3, 4, -3]});
			board.options.label.autoPosition = true;
			board.options.point.size = 1;
var A = board.create('point' , [-1.2,-2], {color:  'orange' , size: 4 });
var B = board.create('point',  [0.25,-0.5], {color:  'orange' , size: 4 });
var hexagon = board.create('regularpolygon', [A,B, 6]);
var D = hexagon.vertices[3];
</script>

{lang=EN} to determine the center Q of the regular hexagon as the center of the circumcircle to the triangle ABD:
{/lang}

{lang=CZ} pro určení středu pravidelného šestiúhelníku Q jako středu kružnice opsané trojúhelníku ABD:
{/lang}

{lang=SI} Zdaj lahko z ukazom circumcenter določimo središče krožnice skozi oglišča A, B in D. {/lang}

{lang=DE} um den Mittelpunkt Q des regulären Sechsecks als Mittelpunkt des Umkreises des Dreiecks ABD zu bestimmen: {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:300px;"></div>
<script>
var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-4, 3, 4, -3]});
			board.options.label.autoPosition = true;
			board.options.point.size = 1;
var A = board.create('point' , [-1.2,-2], {color:  'orange' , size: 4 });
var B = board.create('point',  [0.25,-0.5], {color:  'orange' , size: 4 });
var hexagon = board.create('regularpolygon', [A,B, 6]);
var D = hexagon.vertices[3];
var Q = board.create('circumcenter',  [A, B, D], {name:'Q'});
</script>

{lang=EN} In an analogous way, we then create an equilateral triangle BGH with center R:
{/lang}

{lang=CZ} Analogicky sestrojíme rovnostranný trojúhelník BGH se středem R:
{/lang}

{lang=SI} Analogno konstruiramo pravilni trikotnik BGH s središčem R: {/lang}

{lang=DE} Genauso können wir das gleichseitige Dreieck BGH mit Mittelpunkt R konstruieren: {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:300px;"></div>
<script>
var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-4, 3, 4, -3]});
			board.options.label.autoPosition = true;
			board.options.point.size = 1;
var A = board.create('point' , [-1.2,-2], {color:  'orange' , size: 4 });
var B = board.create('point',  [0.25,-0.5], {color:  'orange' , size: 4 });
var hexagon = board.create('regularpolygon', [A,B, 6]);
var D = hexagon.vertices[3];
var Q = board.create('circumcenter',  [A, B, D], {name:'Q'});
var G = board.create('point', [3,-2],  {name: 'G', color: 'orange' , size: 4 });
var rtr = board.create('regularpolygon',  [B, G, 3]);
var H = rtr.vertices[2];
var R = board.create('circumcenter',  [B, G, H], {name: 'R'});
</script>

{lang=EN} Then, we add the triangle AGB, the midpoint P of its side AB and the lines PQ and PR, which we have to prove are always perpendicular:
{/lang}

{lang=CZ} Nakonec doplníme trojúhelník AGB, střed jeho strany AB bod P a přímky PQ a PR, jejichž kolmost je předmětem důkazu: {/lang}

{lang=SI} Potem konstruiramo trikotnik AGB, razpolovišče P daljice AB in premici PQ ter PR, za kateri moramo pokazati, da sta med seboj pravokotni:

{/lang}

{lang=DE} Dann legen wir das Dreieck AGB, den Mittelpunkt P seiner Seite AB und die Geraden PQ und PR an, für die zu beweisen ist, dass sie immer aufeinander senkrecht stehen. {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:300px;"></div>
<script>
var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-4, 3, 4, -3]});
			board.options.label.autoPosition = true;
			board.options.point.size = 1;
var A = board.create('point' , [-1.2,-2], {color:  'orange' , size: 4 });
var B = board.create('point',  [0.25,-0.5], {color:  'orange' , size: 4 });
var hexagon = board.create('regularpolygon', [A,B, 6]);
var D = hexagon.vertices[3];
var Q = board.create('circumcenter',  [A, B, D], {name:'Q'});
var G = board.create('point', [3,-2],  {name: 'G', color: 'orange' , size: 4 });
var rtr = board.create('regularpolygon',  [B, G, 3]);
var H = rtr.vertices[2];
var R = board.create('circumcenter',  [B, G, H], {name: 'R'});
var tr = board.create('polygon',  [A, G, B], {color: 'pink'});
var P = board.create('midpoint', [A, G], {name: 'P'});
var q = board.create('line', [P, Q], {name: 'q', withLabel: true});
var r = board.create('line', [P, R], {name: 'r', withLabel: true});
</script>

{lang=EN} Finally, we can identify the angle RPQ, the rightness of which we have to prove. JSXGraph recognizes it as a right angle, so it marks it accordingly, as can be seen in figure above:
{/lang}

{lang=CZ} Nakonec můžeme zobrazit předmětný úhel RPQ. JSXGraph ho identifikuje jako pravý úhel a proto ho příslušným způsobem označí, jak vidíme na obrázku výše:
{/lang}

{lang=SI} Na koncu moramo samo še identificirati kot RPQ, za katerega JSXGraph prepozna, da je pravi in ga na ustrezen način označi (glej sliko zgoraj): {/lang}

{lang=DE} Schließlich zeichnen wir den Winkel RPQ, für den zu zeigen ist, dass es sich immer um einen rechten Winkel handelt. JSXGraph erkennt ihn als rechten Winkel, deshalb wird er dementsprechend mit einem kleinen Quadrat kennzeichnet, wie in der obigen Zeichnung zu sehen ist. {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:300px;"></div>
<script>
var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-4, 3, 4, -3]});
			board.options.label.autoPosition = true;
			board.options.point.size = 1;
var A = board.create('point' , [-1.2,-2], {color:  'orange' , size: 4 });
var B = board.create('point',  [0.25,-0.5], {color:  'orange' , size: 4 });
var hexagon = board.create('regularpolygon', [A,B, 6]);
var D = hexagon.vertices[3];
var Q = board.create('circumcenter',  [A, B, D], {name:'Q'});
var G = board.create('point', [3,-2],  {name: 'G', color: 'orange' , size: 4 });
var rtr = board.create('regularpolygon',  [B, G, 3]);
var H = rtr.vertices[2];
var R = board.create('circumcenter',  [B, G, H], {name: 'R'});
var tr = board.create('polygon',  [A, G, B], {color: 'pink'});
var P = board.create('midpoint', [A, G], {name: 'P'});
var q = board.create('line', [P, Q], {name: 'q', withLabel: true});
var r = board.create('line', [P, R], {name: 'r', withLabel: true});
var angle = board.create('angle', [R, P, Q], {radius: 0.4, color: 'red', fillOpacity: 0 , name:'&varphi;' });
</script>

{lang=EN} If this symbolic expression of the right angle is not enough for us, we can enter the code to display the size of the respective angle: {/lang}

{lang=CZ} Pokud nám takovéto symbolické vyznačení pravého úhlu nepostačuje, můžeme použít následující kód pro zobrazení číselné hodnoty jeho velikosti:
{/lang}

{lang=SI} Če nismo zadovoljni s simbolično predstavitvijo pravega kota, lahko zapišemo njegovo velikost še v stopinjah:
{/lang}

{lang=DE} Falls die symbolische Kennzeichnung des rechten Winkels noch nicht deutlich genug ist, können wir noch den Wert des Winkels auszugeben: {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:300px;"></div>
<script>
var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-4, 3, 4, -3]});
			board.options.label.autoPosition = true;
			board.options.point.size = 1;
var A = board.create('point' , [-1.2,-2], {color:  'orange' , size: 4 });
var B = board.create('point',  [0.25,-0.5], {color:  'orange' , size: 4 });
var hexagon = board.create('regularpolygon', [A,B, 6]);
var D = hexagon.vertices[3];
var Q = board.create('circumcenter',  [A, B, D], {name:'Q'});
var G = board.create('point', [3,-2],  {name: 'G', color: 'orange' , size: 4 });
var rtr = board.create('regularpolygon',  [B, G, 3]);
var H = rtr.vertices[2];
var R = board.create('circumcenter',  [B, G, H], {name: 'R'});
var tr = board.create('polygon',  [A, G, B], {color: 'pink'});
var P = board.create('midpoint', [A, G], {name: 'P'});
var q = board.create('line', [P, Q], {name: 'q', withLabel: true});
var r = board.create('line', [P, R], {name: 'r', withLabel: true});
var angle = board.create('angle', [R, P, Q], {radius: 0.4, color: 'red', fillOpacity: 0 , name:'&varphi;' });
			board.create('text', [-3, -3, 
				function () {return '&theta;_1 = ' + (arc2.Value() * 180 /Math.PI).toFixed(1) + '&deg;';}
				]); 
</script>

{lang=EN} The task solution code is now complete. {/lang}

{lang=CZ} Kód uvedeného dynamického obrázku je nyní kompletní. {/lang}

{lang=SI} Koda rešitve je s tem zaključena. {/lang}

{lang=DE} Damit ist die Zeichnung fertiggestellt. {/lang}

{lang=EN}

Intersections

Sometimes we want to distinguish some intersections of our objects (lines and circles). Usually we have to compute the intersections, but JSXGraph has very convenient objects Intersection which we can use, to do just that. In order to create an intersection, we need to use two lines, two circles or mix of them. We cannot use other objects to create this object. {/lang}

{lang=SI}

Presečišča

Včasih želimo izračunati ali narisati presečišča med objekti. To lahko rešimo računsko, lahko pa uporabimo objekt v JSXGraphu imenovan Intersection. S pomočjo tega lahko določamo presečišča med dvema premicama, dvema krožnicama, ali pa med krožnico in premico. Med drugimi objekti to ni mogoče. {/lang}

{lang=CZ}

Průsečíky

Pro určení průsečíků přímek a kružnic můžeme v JSXGraphu použít přímo objekt Intersection (průsečík), nemusíme tyto průsečíky počítat. Pro jeho zadání potřebujeme dvě přímky, dvě kružnice nebo jednu přímku a jednu kružnici. Jiné objekty pro určení jejich průsečíku nelze použít.

{/lang}

{lang=DE}

Schnittpunkte

Hin und wieder wollen wir einige Schnittpunkte unserer Objekte (Geraden und Kreise) anzeigen. Normalerweise müssten wir die Schnittpunkte berechnen, aber JSXGraph stellt das recht komfortable Objekt Intersection dafür bereit. Um einen Schnittpunkt zu erzeugen, benötigen wir zwei Geraden / oder Strecken, zwei Kreise oder eine Mischung der beiden. Andere Objekte können dafür nicht verwendet werden. {/lang}

<div id="jxgbox" class="jxgbox" style="width:500px; height:200px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-5, 2, 5, -2],keepAspectRatio:true, showCopyright:false, showNavigation:false });
 var p = board.create('point',[-2,0],{name:"A"});
 var q = board.create('point',[-1,-1],{name:"B", visible:false});
 var r = board.create('point',[0,0],{name:"C"});
 var circle1 = board.create('circle', [p,q]);
 var circle2 = board.create('circle', [r,p]);
 var inter1 = board.create('intersection',[circle1,circle2,0],{name:'I_1'});
 var inter2 = board.create('intersection',[circle1,circle2,1],{name:'I_2'});
 var line = board.create('line',[inter1,inter2]);
</script>

{lang=EN} After we created points and two circles, we created two objects - intersections.

In var inter1 = board.create('intersection',[circle1,circle2,0],{name:'I_1'}); we used a third argument 0 which we use in the case if there are two intersecting points and we decide which intersection we will use (with $0$ and $1$). Notice that in {name:'I_2'}) we used underscore in the name. This is $LATEX$ notation and can be used for the labels to typeset beautiful math.

As last we created new line var line = board.create('line',[inter1,inter2]); with the intersection objects. We can therefore use newly created objects as regular points in our constructions. {/lang}

{lang=SI} Ko smo ustvarili točke in dva kroga, smo konstruirali dva objekta tipa intersection.

V vrstici var inter1 = board.create('intersection',[circle1,circle2,0],{name:'I_1'}); določimo presečišče med dvema krogoma in dodamo še tretji parameter, ki ima vrednost 0. To uporabimo takrat, ko je presečišč med objekti več in moramo določiti eno izmed njiju (če sta presečišči dve, imata vrednosti $0$ in $1$). Za definicijo drugega presečišča smo zato zapisali vrednost 1. Opazimo lahko, da smo v imenu {name:'I_2'}) uporabili zapis z podčrtajem. To je $LATEX$ notacija in se uporablja za lep zapis matematičnih znakov in simbolov.

Na koncu ustvarimo še novo premico var line = board.create('line',[inter1,inter2]);, ki gre skozi presečišči. Torej presečišča so tudi točke, ki jih lahko uporabljamo za nadaljevanje konstrukcije.

{/lang}

{lang=CZ} Po vytvoření bodů a dvou kružnic jsme definovali dva objekty typu průsečík - intersections.

V kódu var inter1 = board.create('intersection',[circle1,circle2,0],{name:'I_1'}); jsme použili za výčtem dvou kružnic třetí argument, zde konkrétně s hodnotou 0, který zadáváme v případě, že objekty mají dva průsečíky a my chceme ovlivnit, který z nich použijeme (uvedením $0$ nebo $1$). Za povšimnutí stojí, že jsme v atributu {name:'I_2'}) použili ve jménu symbol podtržítka pro zápis dolního indexu. Jedná se o syntaxi typografického systému $LATEX$, která může být v JSXGraphu použita při zápisu jmenovek pro dosažení lépe vypadajícího matematického zápisu.

Nakonec jsme definovali novou přímku var line = board.create('line',[inter1,inter2]); procházející získanými průsečíky. Z toho je vidět, jak můžeme nově získané objekty hned použít jako určující body pro další konstrukci.

{/lang}

{lang=DE} Nachdem wir zwei Punkte und zwei Kreise angelegt haben, können wir zwei intersection-Objekte erzeugen.

In var inter1 = board.create('intersection',[circle1,circle2,0],{name:'I_1'}); haben wir als drittes Argument 0 angegeben. Das ist von Bedeutung, wenn durch den Schnitt zweier Objekte zwei Schnittpunkte existieren und wir festlegen wollen, welchen der beiden wir verwenden (durch Angabe der Werte $0$ und $1$).

Beachte: in der Angabe {name:'I_2'}) wurde ein Unterstrich verwendet. Das ist $LaTeX$-Notation und kann bei Bezeichner eingesetzt werden um schöne Mathematik-Formelschreibweise zu erzeugen.

{lang=EN}

Angles

When we need to emphasize a specific angle in our construction, we can do this with object Angle. As an input we need to provide three points $p1, p2, p3$ and the angle is drawn counterclockwise from $p1$ to $p3$ around $p2$. Other combinations include two lines and two directions (by +/- 1) or a line and two coordinates. {/lang}

{lang=SI}

Koti

Kadar želimo povdariti določen kot v naši konstrukciji, lahko to storimo z objektom Angle. Kot vhodne parametre lahko podamo tri točke $p_1$, $p_2$ in $p_3$, potem se kot nariše v obratni smeri urinega kazalca od $p_1$ do $p_3$ okoli $p_2$. Drugi način je s pomočjo dveh premic in dveh smeri (+/- 1), ali pa se zapiše premica in dve točki. {/lang}

{lang=CZ}

Úhly

Pro zvýraznění konkrétních úhlů v konstrukci nabízí JSXGraph objekt Angle (Úhel). Jako vstupní údaje je třeba zadat tři body $p1, p2, p3$, úhel je pak vykreslen v kladném smyslu (tj. proti směru pohybu hodinových ručiček) od bodu $p1$ (bod na počátečním rameni) do bodu $p3$ (bod na koncovém rameni), kolem $p2$ (vrchol).

Dalšími možnostmi zadání vstupních údajů pro zobrazení úhlu jsou dvě přímky a dva směry (ve tvaru +/- 1) nebo dvě přímky a dva body (kolmý průmět každého z těchto bodů na jemu příslušnou přímku, dle pořadí v zápisu, určuje polopřímku, která je ramenem úhlu). {/lang}

{lang=DE}

Winkel

Wenn Winkel in unserer Konstruktion gekennzeichnet werden sollen, kann dies mit dem Objekt Angle bewerkstelligt werden. Als Eingabe müssen wir drei Punkte $p1, p2, p3$ bereitstellen. Der Winkel wird dann gegen den Uhrzeigersinn von $p1$ nach $p3$ um $p2$ markiert.

Andere Möglichkeiten zur Winkelauszeichnung sind, zwei Geraden und zwei Richtungen (mit +/-1) oder eine Gerade und zwei Koordinaten zu verwenden. {/lang}

<div id="jxgbox" class="jxgbox" style="width:500px; height:200px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-5, 2, 5, -2],keepAspectRatio:true, showCopyright:false, showNavigation:false });
 var p = board.create('point',[-2,0],{name:"A"});
 var q = board.create('point',[1,1.5],{name:"B"});
 var r = board.create('point',[1,-1],{name:"C"});
 var line1 = board.create('line',[p,q]);
 var line2 = board.create('line',[p,r]);
 var angle1 = board.create('angle',["C", "A", "B"], {radius:2});
 var angle2 = board.create('angle',[line2,line1,-1,-1], {radius:1,color:'green'});
 var angle3 = board.create('angle',[line2,line1,1,1], {radius:1,color:'blue'});
</script>

{lang=EN}

In this example we first created three points and then through them created two lines with common/intersection point $A$.

Then we created first angle with var angle = board.create('angle',[r, p, q], {radius:2}); using three points. Remember, when defining angle with three points we have to provide them in counterclockwise order, where the angle is centered by the second point. Additionaly, we set an attribute radius to $2$, which tells JSXGraph how big the arc of an angle should be.

Then the second angle $\beta$ was created using two lines and two directions (+/- 1) with following line var angle2 = board.create('angle',[line2,line1,-1,-1], {radius:1,color:'green'});. This line presents another possible method to input the parameters of an angle. We can combine them differently to get different angles at the intersection point $A$.

Last angle is only a variation of angle2 with different directions and as a result we can see that angle1 and angle3 describe the same angle but with different input parameters. {/lang}

{lang=SI} V tem primeru smo najprej ustvarili tri točke in skozi njih dve premici s skupno točko $A$.

Prvi kot smo konstruirali z var angle = board.create('angle',[r, p, q], {radius:2});, torej s pomočjo treh točk. Še enkrat opomnimo, da je vrstni red točk pomemben, središče kota je vedno sredinska točka. Dodatno smo uporabili atribut radius:2, ki pove velikost loka, ki nakazuje kot.

Potem smo dodali drugi kot $\beta$ s pomočjo dveh premic in dveh smeri: var angle2 = board.create('angle',[line2,line1,-1,-1], {radius:1,color:'green'});

Zadnji kot je podoben prejšnjemu, vendar z drugačnimi smermi. Opazimo lahko, da sta angle1 in angle3 enaka, vendar smo ju opisali z različnimi parametri.

{/lang}

{lang=CZ} Nejprve jsme vytvořili tři body A, B, C a jimi určené dvě přímky se společným bodem $A$.

První úhel (programem označený jako $\alpha$) jsme definovali pomocí těchto tří bodů. Zapsali jsme ho kódem var angle1 = board.create('angle',["C", "A", "B"], {radius:2}); K pořadí uvedení bodů připomeňme, že úhel zadáváme třemi body ve směru proti pohybu hodinových ručiček, přitom jako prostřední uvádíme vrchol úhlu. Nakonec jsme uvedli atribut poloměru oblouku úhlu radius s hodnotou $2$, abychom JSXGraphu sdělili, jak velkým obloukem má úhel vykreslit.

Kódem var angle2 = board.create('angle',[line2,line1,-1,-1], {radius:1,color:'green'}); byl vytvořen druhý úhel $\beta$, užitím dvou přímek a stanovením směrů (+/- 1) jeho ramen, která na těchto přímkách leží. Jedná se o další možnost zadání úhlu. Různými kombinacemi hodnot (+/- 1) směrů můžeme vyjádřit všechny možné úhly s vrcholem v $A$.

Poslední úhel $\gamma$ je pouhou variací předchozího úhlu $\beta$ (též angle2) získanou právě změnou směrů ramen. Vidíme tak, že proměnné angle1 a angle3 popisují stejný úhel, avšak s použitím různých vstupních údajů.

{/lang}

{lang=DE} In diesem Beispiel werden zuerst drei Punkte angelegt, sowie zwei Geraden durch diese Punkte mit gemeinsamen Punkt $A$.

Der erste Winkel wird mittels var angle = board.create('angle',[r, p, q], {radius:2}); unter Verwendung der drei Punkte gezeichnet. Wir erinnern uns, bei der Definition des Winkels durch drei Punkte werden diese gegen den Uhrzeigersinn angegeben, wobei der Winkel um den zweiten Punkt verläuft. Zusätzlich setzen wir das Attribut radius auf $2$, was JSXGraph anweist, wie groß der Kreisbogen eines Winkels gezeichnet werden soll.

Der zweite Winkel $\beta$ wird durch Angabe zweier Geraden und zweier Richtungen (+/- 1) angelegt: var angle2 = board.create('angle',[line2,line1,-1,-1], {radius:1,color:'green'});. Durch die Kombinationen der Richtungen können wir die vier verschiedenen Winkel der beiden Geraden kennzeichnen.

Der dritte Winkel ist eine Variation von angle2 mit anderen Richtungen mit dem Resultat, dass angle1 und angle3 den gleichen Winkel kennzeichnen, aber unterschiedliche Eingabeparameter verwenden. {/lang}

{lang=EN}

Curves

Curves in JSXGraph does not mean just curves from functions or polynomials, but also parametric curves, polar curves or data plots. In our example we will show how to use data for data plotting, for other uses please check the API documentation. {/lang}

{lang=SI}

Krivulje

Krivulja v JSXGraphu ne pomeni samo graf funkcije, ampak tudi parametrična krivulja, polarna krivulja ali grafični prikaz podatkov. V tem primeru bomo pokazali uporabo podatkov za prikaz poligonske črte oziroma črtnega diagrama. {/lang}

{lang=CZ}

Křivky

Objekt křivka (Curve) v JSXGraphu nezahrnuje jenom grafy funkcí nebo polynomů, ale také parametrické křivky, křivky definované v polárních souřadnicích nebo různé grafické reprezentace dat. Následujícím příkladem ilustrujeme užití objektu Curve ke grafické reprezentaci dat. Další možnosti tohoto objektu viz JSXGraph Reference. {/lang}

{lang=DE}

Kurven

Kurven in JSXGraph umfassen nicht nur Graphen von Funktionstermen oder Polynomen, sondern auch parametrische Kurven, Polarkurven oder Datenplots. In unserem Beispiel zeigen wir wie Datenplots erzeugt werden können. Für die anderen Kurventypen verweisen wir auf die API-Dokumentation. {/lang}

<div id="jxgbox" class="jxgbox" style="width:500px; height:200px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-1, 10, 11, -2], axis:true, showCopyright:false, showNavigation:false });
 var x = [1,2,3,4,5,6,7,8,9,10];
 var y = [8.4,1,0.1,9,3.3,3.3,4.5,8,9,4];
 var curve = board.create('curve',[x,y],{curveType:'plot'});
</script>

{lang=EN} In this example we had to change the bounding box of the board in order to accommodate the data. Otherwise not all points will be visible.

To draw a data plot we first need two lists of data. In our case we used two lists x and y and filled them with numbers. But it is not the only way to obtain the data (e.g. see this example). Finally we had to set the type of curve using attribute curveType. {/lang}

{lang=SI} Za začetek smo morali spremeniti velikost objekta bounding box, da bodo vsi podatki vidni. Za risanje grafa potrebujemo dva seznama podatkov. Uporabili smo seznama xin y, ki smo ju napolnili s števili. To ni edini način zapisovanja podatkov, za več glejte primer). Na koncu samo določimo tip krivulje z atributom curveType.

{/lang}

{lang=CZ} V tomto příkladu jsme především upravili nastavení nákresny, aby více odpovídala potřebám zobrazení daných dat. Kromě změny rozsahu souřadnic, aby byly vidět všechny body, jsme mimo jiné atributem axis s hodnotou true zajistili zobrazení souřadnicových os.

Pro grafické zobrazení dat potřebujeme dva datové seznamy. V uvedeném příkladě jsou použity seznamy x a y, vyplněné čísly. To ale není jediný způsob zadání dat (viz např. tento příklad).

Způsob zobrazení křivky je nastaven pomocí atributu curveType. {/lang}

{lang=DE} In diesem Beispiel passen wir die bounding box an, damit alle Daten sichtbar sind.

Um einen Datenplot zu erstellen, benötigen wir zwei Listen für die $x$- und $y$-Koordinaten der Datenpunkte. In unserem Fall verwenden wir zwei Listen x and y und füllen diese mit Zahlen. Das ist aber nicht die einzige Möglichkeit, Daten zu übergeben, siehe dieses Beispiel. Zuletzt geben wir noch den Kurventyp mit dem Attribut curveType an. {/lang}

{lang=EN}

Drawing mathematical functions

In the constructions we often need to draw mathematical functions like sine or cosine, polynomials or other known functions. JSXGraph provides a convenient method for drawing such functions. Let's look at the example. {/lang}

{lang=SI}

Risanje funkcij

V konstrukcijah pogosto želimo narisati grafe znanik funkcij kot na primer sinus ali kosinus, polinome, itd. JSXGraph ponuja priročno metodo za risanje grafov. Poglejmo primer. {/lang}

{lang=CZ}

Zobrazení grafu funkce

JSXGraph poskytuje pohodlný způsob zobrazování grafů funkcí, např. sinu, kosinu, algebraických funkcí, ale i dalších známých funkcí.

{/lang}

{lang=DE}

Funktionsgraphen

In vielen Konstruktionen benötigen wir Graphen von mathematische Funktionen, wie z.B. $\sin$, $\cos$, Polynome oder andere bekannte Funktionen. JSXGraph stellt eine komfortable Möglichkeit bereit, derartige Funktionen zu zeichnen. Wollen wir uns ein Beispiel ansehen: {/lang}

<div id="jxgbox" class="jxgbox" style="width:300px; height:300px; margin:auto"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-4, 4, 4, -4], axis:true,  showCopyright:false, showNavigation:false });
 var graph1 = board.create('functiongraph', [function(x){return Math.sin(x);}, -Math.PI, Math.PI],{name:'sin(x)', withLabel:true});
 var graph2 = board.create('functiongraph', [function(x){return x*x-2;}, -3, 3],{name:'x^2 - 2', withLabel:true, strokeColor:'red'});
</script>

{lang=EN} In this example we first changed the properties of div and set the width and height to form a square area, because we wanted a nicer looking construction (another possibility would be to use attribute keepAspectRatio in initBoard()). Then we created two functions.

To draw a $\sin (x)$ function we used functiongraph as a type var graph1 = board.create('functiongraph', .
But what follows is something new. Let us look closely at [function(x){return Math.sin(x);},-Math.PI,Math.PI]. With type functiongraph we told JSXGraph that we will be drawing a function on some interval, therefore we need to provide the function we want to draw. function(x){return Math.sin(x);} does just that. Here we use anonymous function function(x) where we provide parameter x, that is used by JSXGraph to provide x values from the interval we have set with the second and third element of the list. In our case this is -Math.PI, Math.PI. Now we have to define a function that will return a value ($y-coordinate$) for the given $x$. This was done by {return Math.sin(x);}. We have to use the reserved word return which is followed by a function, in our case Math.sin(x). We end this with ;} which is used to end the statement and the function.

In the second graph2 we have drawn a quadratic function {return x*x-2;} on the interval -3, 3. We also used some attributes which we already explained on previous pages.

Note: For the sine function we used Javascript Math object.

Alternatively, we could input the function term as string in the form ['sin(x)',-Math.PI,Math.PI]. Then, the JSXGraph internal language JessieCode is used (see the JessieCode chapter) which "understands" the usual math notation. Another example would be ['x^3',-5,5] as a variant to [function(x){return xxx;},-5,5]`. {/lang}

{lang=SI} Na začetku smo rahlo spremenili lastnosti div in nastavili višino in širino na isto vrednost, da bo naša risalna površina kvadrat. Potem smo ustvarili dva grafa.

Za risanje grafa funkcije $\sin (x)$ smo uporabili tip functiongraph v vrstici var graph1 = board.create('functiongraph', .
Kar sledi temu zapisu pa je nekaj novega. Oglejmo si najprej zapis [function(x){return Math.sin(x);},-Math.PI,Math.PI]. Ko smo navedli tip, smo JSXGraphu povedali, da mora narisati neko funkcijo na intervalu. Zato je potrebno podati funkcijo in pa interval. Funkcijo zapišemo z function(x){return Math.sin(x);}, interval pa kot -Math.PI,Math.PI. Uporabili smo anonimno funkcijo function(x) s parametrom x, kjer x zavzame vse vrednosti iz podanega intervala. Zdaj pa moramo definirati specifično funkcijo, ki bo vrnila vrednost (koordinato $y$) pri danem $x$-u. To storimo z {return Math.sin(x);}.

V drugem grafu je postopek podoben. Za konkretno funkcijo uporabimo {return x*x-2;}, kar je kvadratna funkcija, interval pa zapišemo kot -3, 3.

Opomba: za funkcijo sinus smo uporabili objekt Javascript Math.

Alternativno bi lahko zapisali funkcijo v obliki ['sin(x)',-Math.PI,Math.PI]. Potem bi notranji jezik JSXGrapha imenovan JessieCode to razumel kot standardno matematično notacijo. Podoben primer bi bil zapis ['x^3',-5,5] namesto oblike [function(x){return x*x*x;},-5,5]. {/lang}

{lang=CZ}

V tomto příkladě jsme nejprve změnili vlastnosti bloku div, konkrétně jsme nastavili šířku (width) a výšku (height) nákresny tak, aby měla čtvercový tvar (další možností by bylo použití atributu keepAspectRatio ve funkci initBoard(), viz kapitola 3.6 Kružnice). Potom jsme zadali zobrazení grafů dvou funkcí.

Pro zobrazení grafu funkce $\sin (x)$ jsme použili objekt typu functiongraph známým způsobem var graph1 = board.create('functiongraph', ..., ale to, co následuje, je něco nového.

Pojďme se detailně zaměřit na část kódu [function(x){return Math.sin(x);},-Math.PI,Math.PI]. Uvedením typu functiongraph jsme JSXGraph informovali o tom, že budeme zobrazovat graf funkce na nějakém intervalu. Nejprve parametrem function(x){return Math.sin(x);} zadáme výraz $\sin (x)$ definující hodnotu funkce pro dané $x$. Užitím anonymní funkce function(x) zavedeme parametr x, kterému JSXGraph přiřazuje hodnoty ($x-souřadnice$) z intervalu, jehož meze jsou dány druhým a třetím prvkem seznamu parametrů, tj. hodnotami -Math.PI, Math.PI. Argumentem {return Math.sin(x);} je pro JSXGraph definována funkce, která pro dané $x$ vrátí příslušnou funkční hodnotu ($y$-souřadnici). Museli jsme použít klíčové slovo return následované příslušnou funkcí, v našem případě Math.sin(x). Zadání funkce zakončíme znakem ; a ukončíme závorku }.

Druhý graf graph2 přísluší kvadratické funkci {return x*x-2;} na intervalu -3, 3. Samozřejmě, k nastavení vzhledu grafů používáme i atributy, které byly představeny v předchozích kapitolách.

Poznámka: Pro funkci sinus byla použita knihovna Javascript Math. {/lang}

{lang=DE} In diesem Beispiel wurde zuerst die Größe des div-Elementes durch Setzen der Höhe und Breite so verändert, dass es quadratisch ist. Denn wir wollen, dass die Funktionsgraphen im richtigen Verhältnis angezeigt werden (eine andere Möglichkeit wäre, keepAspectRatio in initBoard() zu verwenden).

Danach werden zwei Funktionen gezeichnet: Um $\sin (x)$ zu zeichnen, verwenden wir functiongraph als Objekttyp var graph1 = board.create('functiongraph', .
Was danach folgt, ist neu. Betrachten wir den Ausdruck [function(x){return Math.sin(x);},-Math.PI,Math.PI] genauer. Mit dem Typ functiongraph haben wir JSXGraph mitgeteilt, dass wir eine Funktion in einem gewissen Intervall zeichnen wollen. Deshalb müssen wir nun die Funktion angeben, die gezeichnet werden soll. Dies geschieht durch function(x){return Math.sin(x);}.

Hier nützen wir das JavaScript-Konzept einer anonymen Funktion durch Angabe von function(x) mit einem Parameter x. Dieser wird von JSXGraph verwendet, um x-Werte aus dem Intervall zu übergeben, das wir mit dem zweiten und dritten Element der Liste spezifizieren. In unserem Fall sind die Intervallgrenzen -Math.PI, Math.PI. Nun haben wir noch die JavaScript-Funktion zu definieren, die jeweils zu einem gegebenem $x$ einen Wert (die $y$-Koordinate) zurückgibt. Dies geschieht durch {return Math.sin(x);}. Wir verwenden den reservierten Ausdruck return gefolgt durch einen Funktionsausdruck, in unserem Fall Math.sin(x). Der Ausdruck wird durch ;} beendet.

Im zweiten Funktionsgraph graph2 zeichnen wir die quadratische Funktion {return x*x-2;} im Intervall -3, 3. Zudem verwenden wir wieder Attribute, die wir aber bereits alle aus den vorhergehenden Kapiteln kennen.

Beachte: Für die Sinus-Funktion verwenden wir das JavaScript Math-Objekt.

Da die Verwendung einer JavaScript-Funktion Math.sin()nicht besonders komfortabel ist, gibt es die Alternative, den Funktionsterm als String in der Form ['sin(x)',-Math.PI,Math.PI] anzugeben. Dann wird die JSXGraph-eigene Sprache JessieCode verwendet (siehe das Kapitel zu JessieCode), die die übliche Mathematik-Schreibweise "versteht". Ein anderes Beispiel wäre ['x^3',-5,5] als Alternative zu [function(x){return x*x*x;},-5,5]. {/lang}

{lang=EN}

Animating

Although creating points, lines and also drawing can be very useful, the power of JSXGraph shows when we want our construction to not be fixed, but used to simulate or demonstrate something with movement or animation. In this chapter we will learn

• how to move objects
• how to "glue" objects to other objects (e.g points on the lines)
• how to create sliders
• how to transform objects (scaling, rotating, etc). {/lang}

{lang=SI}

Animiranje

Čeprav je risanje točk, premic in krivulj pogosto zelo koristno, pa se prava korist JSXGrapha pokaže takrat, ko želimo imeti dinamično sliko, ki simulira gibanje ali animacijo. V tem poglavju se bomo naučili, kako

• premikati objekte,
• prilepiti objekte na druge objekte,
• ustvariti drsnike,
• preoblikovati objekte (povečati, rotirati,...). {/lang}

{lang=CZ}

Animace

I když kreslení bodů, přímek a dalších objektů, spolu s jejich spojováním do dynamických konstrukcí, je užitečné, skutečná síla JSXGraphu se projeví v dynamických konstrukcích, v nichž simulujeme nebo demonstrujeme nějaký jev.
V této kapitole se naučíme

• jak pohybovat s objekty,
• jak je přichytávat ("glue") k jiným objektům (např. body k přímkám),
• jak vytvářet posuvníky,
• jak objekty transformovat (změna velikosti, posunutí, otočení atd.). {/lang}

{lang=DE}

Animationen

Although creating points and lines and also drawing can be very useful, the power of JSXGraph lies when we want that our construction are not fixed, but can be used to simulate or demonstrate something. In this chapter we will learn

• how to move objects
• how to "glue" objects to other objects (e.g points on the lines)
• how to create sliders
• how to transform objects (scaling, rotating, etc). {/lang}

{lang=EN}

Moving objects

Sometimes we want to move points to explain or present some concept. We can use this to animate the point by moving to a final point (using method moveTo()) or only visiting some point and returning back to the start. We will use both methods in the next example. {/lang}

{lang=SI}

Premikanje objektov

Kadar želimo razložiti kakšne težje koncepte, nam statična slika ne pomaga in bi želeli videti gibanje. Najbolj preprosta primera premika sta premik točke do nekega mesta in vrnitev na začetek. Oba bomo pokazali v spodnjem primeru. {/lang}

{lang=CZ}

Pohybování s objekty

Pro ilustraci nebo vysvětlení některých jevů potřebujeme mít někdy možnost cíleně pohybovat s vybranými body obrázku. Můžeme například bod jednoduše přemístit do daného cílového místa (použitím metody moveTo()), nebo ho někam pošleme, aby se potom vrátil zpět do výchozího místa. V následujícím příkladu použijeme oba tyto režimy pohybu. {/lang}

<div id="jxgbox" class="jxgbox" style="width:500px; height:200px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-4, 4, 4, -4],keepAspectRatio:true, showCopyright:false, showNavigation:false });
 var p = board.create('point',[-1,0],{name:"A"});
 var q = board.create('point',[3,2],{name:"B"});
 var button1 = board.create('button',[2,3,'Start B', function(){q.visit([3,-2],1800,2)}]);
 var button2 = board.create('button',[-3,3,'Move A', function(){p.moveTo([Math.random()*8-4,Math.random()*8-4],500);}]);
</script>

{lang=EN} First three lines are usual, but in the next line var button1 = board.create('button',[2,3,'Start B', function(){q.visit([3,-2],1800,2)}]); we use two new commands.

Let us focus first on the second command: q.visit([3, -2], 1800, 2). Until now we have always used only one method create() which we provided with parameters to create points, etc. on the board. Now we introduce a new method for the point which is called visit(). Its syntax is visit(where, time, options) with three parameters,

• where coordinates of our destination e.g. [3, -2],
• time how long should it take e.g. 1800,
• options in our case how many repetitions of our visit e.g 2.

First command creates a button on a board which click on it triggers some action. The parameters in the list are as follows [x-coordinate, y-coordinate, title on the button, action]. In our case the action was anonymous function with the visit method on point q.

The second button is created in next line, but let us now look at the action more closely which is p.moveTo([Math.random()*8-4,Math.random()*8-4],500);. Here a new method moveTo is used on the point q, which takes only two parameters

• destination coordinates as a list of two elements e.g [Math.random()*8-4,Math.random()*8-4]
• animation time in milliseconds, e.g 500.

For the coordinates we use Math.random method, which creates new random number between 0 and 1 every time we click on the button, then we multiply it by $8$ and subtract $4$. The result will be a number between $-4$ and $4$m which are also the limits of our bounding box. We do the same for both coordinates. As a result our point p ("A") moves across the board randomly. {/lang}

{lang=SI} Prve tri vrstice so enake kot običajno, naslednja vrstica var button1 = board.create('button',[2,3,'Start B', function(){q.visit([3,-2],1800,2)}]); pa vsebuje nekaj novih ukazov.

Podobno kot smo ustvarjali točke, premice in krožnice, lahko ustvarimo tudi gumbe tipa 'button', ki izvedejo neko dejavnost ob kliku. Parametri v seznamu so sledeči: [x-koordinata, y-koordinata, napis na gumbu, dejanje]. Torej položaj gumba, napis in kaj naj stori ob kliku.

V našem primeru želimo, da se ob kliku izvede funkcija function(){q.visit([3,-2],1800,2)}. Tukaj smo klicali nov ukaz, ki se imenuje visit(). Njegov zapis je oblike visit(lokacija, čas, možnosti) s tremi parametri:

• lokacija so koordinate točke, kamor se naj objekt premakne (v našem primeru [3, -2]),
• čas pomeni čas trajanja animacije v milisekundah (1800),
• možnosti pomeni število ponovitev (pri nas je to 2).

V naslednji vrstici smo ustvarili nov gumb s koordinatami -3,3, z napisom 'Move A' in z ukazom function(){p.moveTo([Math.random()*8-4,Math.random()*8-4],500);}. Tukaj smo uporabili novo metodo imenovano moveTo, ki prejme dva parametra:

• koordinate, ki jih zapišemo kot seznam dveh števil,
• čas animacije v milisekundah.

Za koordinate premika smo uporabili metodo Math.random, ki ustvari naključno število med $0$ in $1$. Potem smo jo pomnožili s številom $8$ in odšteli $4$. Rezultat bo vedno naključno število med $-4$ in $4$, tako da bomo ostali znotraj mej našega platna.

{lang=CZ} Význam prvích tří řádků (za značkou <script>) už známe, další řádek var button1 = board.create('button',[2,3,'Start B', function(){q.visit([3,-2],1800,2)}]); ale přináší dva nové příkazy.

Pojďme se nejprve zaměřit na příkaz: q.visit([3, -2], 1800, 2). Dosud jsme používali jenom metodu create(), kterou jsme doplnili náležitými parametry pro zobrazení bodů apod. na nákresnu. Nyní představujeme novou metodu pro nakládání s bodem, která se nazývá visit(). Její syntaxe je visit(místo, doba trvání, volby) s těmito třemi parametry:

• místo (where) souřadnice cíle pohybu, např. [3, -2],
• doba trvání (time) jak dlouho, v milisekundách, to bude trvat, např. 1800,
• volby (options), v našem případě se jedná o počet opakování, např. 2.

Výše uvedený kód čtvrtého řádku vytvoří v nákresně tlačítko, kliknutím na které se spustí nějaká akce. Význam parametrů uvedených v seznamu je následující: [x-souřadnice, y-souřadnice, nápis na tlačítku, akce]. Akcí je v našem případě anonymní funkce aplikující metodu visit na bod q.

Druhé tlačítko je vytvořeno na následujícím řádku. Pojďme se ale detailněji zaměřit na příslušnou akci, což je p.moveTo([Math.random()*8-4,Math.random()*8-4],500);. Zde aplikujeme na bod q novou metodu moveTo, která využívá pouze dva parametry:

• souřadnice cíle jako seznam o dvou složkách, např. [Math.random()*8-4,Math.random()*8-4]
• čas animace v ms, např. 500.

Pro stanovení souřadnic cíle používáme metodu Math.random, která při každém kliknutí na tlačítko generuje náhodné číslo z intervalu od 0 do 1. Toto číslo se pak v našem konkrétním případě násobí $8$ a od výsledku se odečte $4$, aby byla hodnota příslušné souřadnice z rozmezí od $-4$ do $4$, které odpovídá rozsahu nákresny. Tímto způsobem definujeme obě souřadnice cíle pohybu. Výsledným efektem je náhodný pohyb našeho bodu p ("A") po nákresně. {/lang}

{lang=EN}

Example: Proof without words

Area of a parallelogram. The area of a parallelogram equals its base multiplied by its height. Prove it!

To solve the example we will use a dynamic proof without words, see figure below. By this means we will show that the area of a parallelogram equals the area of a rectangle whose base and height are the same as that of the parallelogram. {/lang}

{lang=SI}

Primer: dokaz brez besed

Površina paralelograma. Površina paralelograma je enaka produktu dolžine osnovnice in njegove višine. Dokažite!

Za rešitev problema bomo uporabili metodo dokaz brez besed. To bomo storili tako, da bomo pokazali, da je površina paralelograma enaka površini pravokotnika, ki ima eno stranico enako osnovnici paralelograma, druga stranica pa je enaka višini paralelograma. {/lang}

{lang=CZ}

Příklad: Důkaz beze slov

Obsah rovnoběžníku. Obsah rovnoběžníku je roven součinu velikostí jeho základny a výšky na tuto základnu. Dokažte!

Úkol vyřešíme předložením dynamického důkazu beze slov, viz obrázek níže. Jeho prostřednictvím prokážeme, že obsah rovnoběžníku je stejný jako obsah obdélníku, jehož základna a výška jsou stejné jako u rovnoběžníku. {/lang}

{lang=EN} Programming:

First, we define dimensions, width and height, of the drawing area setting the corresponding properties of the div element: {/lang}

{lang=SI} Programiranje:

Najprej definiramo dimenzije risalne površine z nastavitvijo lastnosti div elementa: {/lang}

{lang=CZ} Programování:

Nejprve stanovíme rozměry, tj. šířku a výšku, nákresny přiřazením náležitých hodnot odpovídajícím atributům prvku div: {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:250px;"></div> 

{lang=EN} Subsequently, at the beginning of the code bounded by the tags <script>, </script>, we determine the Bounding box as follows: {/lang}

{lang=SI} Nadalje določimo naš bounding box tako: {/lang}

{lang=CZ} Následně, na začátku kódu vymezeného tagy <script>, </script>, definujeme rozsahy souřadnicových os zavedených v nákresně: {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:250px;"></div>
<script>
    var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-1, 4, 7, -1]});
</script>

{lang=EN} As an initial sketch, the foundation of the dynamic figure, we draw the fixed parallelogram ABCD that is visible only by its boundary, having no filling: {/lang}

{lang=SI} Kot osnovo naše dinamične slike narišemo paralelogram ABCD, ki ima vidne robove, v notranjosti pa je prazen: {/lang}

{lang=CZ} Jako výchozí motiv, který se stane základem dynamického obrázku, sestrojíme pevný (tj. nepohyblivý) rovnoběžník ABCD, bez výplně, zobrazený pouze svými stranami: {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:250px;"></div>
<script>
    var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-1, 4, 7, -1]});
	var A = board.create('point', [0,0], {name:'A', fixed:true, size:1});
    var B = board.create('point', [4,0], {name:'B', fixed:true, size:1});
    var D = board.create('point', [2,3], {name:'D', fixed:true, size:1});
    var C = board.create('parallelpoint', [A, B, D], {name:'C', size:1});
    var par = board.create('polygon', [A, B, C, D], {color:'blue', fillOpacity: 0});
</script>

{lang=EN} Then, we determine point Q, invisible in the figure, the foot of the line passing through D perpendicular to AB, and use it to define a trapezoid QBCD with blue filling, an invariable part of the intended dynamic figure: {/lang}

{lang=SI} Potem določimo točko Q (ki bo na sliki nevidna) kot nožišče pravokotnice na osnovnico skozi točko D. S tem lahko določimo trapez QBCD z modrim polnilom: {/lang}

{lang=CZ} Jako patu kolmice z vrcholu D na přímku AB určíme bod Q, který je v dynamickém obrázku skryt. Slouží jako čtvrtý vrchol potřebný pro sestrojení modře vybarveného lichoběžníku QBCD, který je nehybnou částí vytvářeného dynamického vizuálního důkazu: {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:250px;"></div>
<script>
    var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-1, 4, 7, -1]});
	var A = board.create('point', [0,0], {name:'A', fixed:true, size:1});
    var B = board.create('point', [4,0], {name:'B', fixed:true, size:1});
    var D = board.create('point', [2,3], {name:'D', fixed:true, size:1});
    var C = board.create('parallelpoint', [A, B, D], {name:'C', size:1});
    var par = board.create('polygon', [A, B, C, D], {color:'blue', fillOpacity: 0});
	var Q = board.create('point', [
                    function(){ return D.X(); },
                    function(){ return A.Y();
            }], {name:'Q', visible:false});
	var tra = board.create('polygon', [Q, B,C,D], {color:'blue', withLines:false, fillOpacity: 0.3});
</script>

{lang=EN} To complete the parallelogram, we create the right triangle MNP, again filled with blue, the moving part of the visual proof without words. To allow its movement the vertices M, N, P will be independent on the other objects of the figure: {/lang}

{lang=SI} Da dopolnimo trapez do paralelograma, ustvarimo še pravokotni trikotnik MNP, spet z modrim polnilom. To bo gibljivi del našega dokaza, zato morajo njegova oglišča biti neodvisna od preostalih objektov na sliki. {/lang}

{lang=CZ} Pro dokončení výplně rovnoběžníku vytvoříme pravoúhlý trojúhelník MNP, opět modře vybarvený, který bude pohyblivou částí vizuálního dynamického důkazu beze slov. Aby se mohl hýbat, vytvoříme jeho vrcholy M, N, P jako body nezávislé na ostatních prvcích obrázku: {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:250px;"></div>
<script>
    var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-1, 4, 7, -1]});
	var A = board.create('point', [0,0], {name:'A', fixed:true, size:1});
    var B = board.create('point', [4,0], {name:'B', fixed:true, size:1});
    var D = board.create('point', [2,3], {name:'D', fixed:true, size:1});
    var C = board.create('parallelpoint', [A, B, D], {name:'C', size:1});
    var par = board.create('polygon', [A, B, C, D], {color:'blue', fillOpacity: 0});
	var Q = board.create('point', [
                    function(){ return D.X(); },
                    function(){ return A.Y();
            }], {name:'Q', visible:false});
	var tra = board.create('polygon', [Q, B,C,D], {color:'blue', withLines:false, fillOpacity: 0.3});
	var M = board.create('point', [0,0], {name:'M', visible:false});
    var N = board.create('point', [function() {return M.X()+2;}, function(){return M.Y();}], {name:'N', visible:false})
    var P = board.create('point', [function() {return M.X()+2;}, function(){return M.Y()+3;}], {name:'P', visible:false})
    var tri = board.create('polygon', [M, N, P], {color:'blue', withLines:false, fillOpacity: 0.3});
</script>

{lang=EN} Finally, we define two buttons to control the movement of the triangle MNP back and forth: {/lang}

{lang=SI} Nato definiramo dva gumba, ki bosta premikala trikotnik MNP naprej ali nazaj: {/lang}

{lang=CZ} Nakonec vytvoříme dvě tlačítka pro ovládání pohybu pravoúhlého trojúhelníku MNP tam a zpět: {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:250px;"></div>
<script>
    var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-1, 4, 7, -1]});
	var A = board.create('point', [0,0], {name:'A', fixed:true, size:1});
    var B = board.create('point', [4,0], {name:'B', fixed:true, size:1});
    var D = board.create('point', [2,3], {name:'D', fixed:true, size:1});
    var C = board.create('parallelpoint', [A, B, D], {name:'C', size:1});
    var par = board.create('polygon', [A, B, C, D], {color:'blue', fillOpacity: 0});
	var Q = board.create('point', [
                    function(){ return D.X(); },
                    function(){ return A.Y();
            }], {name:'Q', visible:false});
	var tra = board.create('polygon', [Q, B,C,D], {color:'blue', withLines:false, fillOpacity: 0.3});
	var M = board.create('point', [0,0], {name:'M', visible:false});
    var N = board.create('point', [function() {return M.X()+2;}, function(){return M.Y();}], {name:'N', visible:false})
    var P = board.create('point', [function() {return M.X()+2;}, function(){return M.Y()+3;}], {name:'P', visible:false})
    var tri = board.create('polygon', [M, N, P], {color:'blue', withLines:false, fillOpacity: 0.3});
	var button1 = board.create('button', [-0.5,3, 'Forth', function(){ M.moveTo([4,0], 1000); }]);
    var button2 = board.create('button', [-0.5,2.5, 'Back', function(){ M.moveTo([0,0], 1000); }]);
</script>

{lang=EN} The task solution code is now complete. {/lang}

{lang=SI} Koda dokaza je s tem končana. {/lang}

{lang=CZ} Kód řešení úlohy je nyní kompletní. {/lang}

{lang=EN}

Sliders

Sliders can be used in various settings, where we want the users to tinker with the values of some variable. In our example we will use a quadratic function. {/lang}

{lang=SI}

Drsniki

Drsniki so koristen dodatek, kadar želimo, da uporabnik sam spreminja vrednosti objektov na sliki. V našem primeru bomo uporabili drsnike na grafu kvadratne funkcije. {/lang}

{lang=CZ}

Posuvníky

Posuvník (slider) můžeme použít v různých situacích, ve kterých chceme, aby měl uživatel možnost bezprostředně měnit hodnotu nějaké proměnné. Pro ukázku použití posuvníků jsme zvolili náležitou úpravu dříve uvedeného příkladu s kvadratickou funkcí. {/lang}

<div id="jxgbox" class="jxgbox" style="width:300px; height:300px; margin:auto"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-8, 8, 8, -8], axis:true,  showCopyright:false, showNavigation:false });
 var a = board.create('slider', [[-7.5, -3], [-4,-3], [-3, 1, 3]], {name:'a', snapWidth: 0.1});
 var c = board.create('slider', [[-7.5, -5], [-4,-5], [-1, 1, 4]], {name:'c',snapWidth: 1});
 var graph2 = board.create('functiongraph', [function(x){return a.Value()*x*x + c.Value();}, -3, 3]);
 var text = board.create('text',[-6,6,function(){return a.Value().toFixed(2)+'\\times x^2'+c.Value()}]);
</script>

{lang=EN} We extended the example with two sliders which now control the quadratic function. But first let us look closer on how we created first slider: var a = board.create('slider', [[-7.5, -3], [-4,-3], [-3, 1, 3]], {name:'a', snapWidth: 0.1});

To create a slider we need to provide following parameters:

• coordinates of the first point of the slider, e.g. [-7.5, -3]
• coordinates of the last point of the slider, e.g. [-4,-3]
• values of the slider as a list [min, start, max], e.g. [-3, 1, 3].

Here we also used atribute snapWidth which tells JSXGraph how fine the steps of the slider should be. Second slider is generated in similar way, except we set the attribute snapWidth to $1$ to generate only integer values.

In last line we now used the values from both sliders and extended our quadratic function with return a.Value()*x*x + c.Value(). We can see, that to get the value of the slider we used the variable name and method Value() e.g. a.Value().

Now the quadratic function is not fixed with the values but can be dynamically changed with the user interaction.

{/lang}

{lang=SI}

Ustvarili smo dva drsnika, ki nadzirata vrednosti v kvadratni funkciji. Poglejmo prvega: var a = board.create('slider', [[-7.5, -3], [-4,-3], [-3, 1, 3]], {name:'a', snapWidth: 0.1});

Zapisati smo morali naslednje parametre:

• koordinate začetka drsnika, torej [-7.5, -3],
• koordinate konca drsnika, torej [-4,-3],
• vrednosti na drsniku v seznamu oblike [min, začetek, max], torej [-3, 1, 3].

Uporabili smo še atribut snapWidth, ki pove JSXGraphu kako fini naj bodo premiki po drsniku. Drugi drsnik je konstruiran na podoben način, le da smo pri atributu snapWidth uporabili vrednost $1$, kar pomeni, da se bo drsnik premikal samo po celih številih (bolj grobo).

V zadnji vrstici smo povezali podatke iz drsnikov z grafom kvadratne funkcije s pomočjo metode Value(), ki vrne trenutno vrednost na drsniku. Funkcija potem izgleda tako function(x){return a.Value()*x*x + c.Value();.

Zdaj funkcija ni fiksna, ampak se njene vrednosti spreminjajo glede na drsnika.

{/lang}

{lang=CZ} Obrázek jsme doplnili dvěma posuvníky, kterými ovládáme koeficienty $a$, $c$ dané kvadratické funkce. Pojďme se podrobně podívat na to, jak jsme vytvořili první posuvník (slider): var a = board.create('slider', [[-7.5, -3], [-4,-3], [-3, 1, 3]], {name:'a', snapWidth: 0.1});

Pro vytvoření posuvníku potřebujeme definovat následující parametry:

• souřadnice počátečního bodu posuvníku, např. [-7.5, -3],
• souřadnice koncového bodu posuvníku, např. [-4,-3],
• určující hodnoty posuvníku formou seznamu [min, start, max], např. [-3, 1, 3].

V příkladu jsme dále použili atribut snapWidth, který stanoví, jak jemný má být krok posuvníku. Druhý posuvník je vytvořen podobným způsobem, kromě toho, že jsme atributu snapWidth přiřadili hodnotu $1$, aby nabýval pouze celočíselných hodnot.

V posledním řádku kódu jsme použili hodnoty obou posuvníků v definici naší kvadratické funkce return a.Value()*x*x + c.Value(). Vidíme zde, že pro získání okamžité hodnoty posuvníku použijeme spojení jména proměnné a metody Value() takto a.Value().

Předpis kvadratické funkce tak už není neměnný, díky posuvníkům může být jeho podoba uživatelem dynamicky měněna. {/lang}

{lang=EN}

Animating with sliders

One great use of a slider is animation. Instead of moving the slider by hand, JSXGraph has a function that can move the slider by itself. In this example we will create a slider and two buttons that can start and stop the animation of an increasing and decreasing circle. {/lang}

{lang=SI}

Animacija z drsniki

Odličen primer uporabe drsnikov je ustvarjanje animacij. JSXGraph ima funkcijo, ki omogoča samodejno premikanje drsnikov, torej jih ne rabimo premikati ročno. V spodnjem primeru bomo ustvarili drsnik in gumbe, ki bodo začeli in ustavili animacijo naraščanja in krčenja kroga. {/lang}

{lang=CZ}Animating with sliders{/lang}

<div id="jxgbox" class="jxgbox" style="width:500px; height:500px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-3, 3, 3, -3],keepAspectRatio:true, showCopyright:false, showNavigation:false });
 var r = board.create('slider',[[-2,-2],[2,-2],[0,1,2]],{name:'r'});
 var A = board.create('point',[0,0.5], {visible:false});
 var button1 = board.create('button', [-2, -2.3, 'Start increasing',function(){r.startAnimation(1, 40, 30)}]);
 var button2 = board.create('button', [-2, -2.6, 'Start decreasing',function(){r.startAnimation(-1, 10, 100)}]);
 var button3 = board.create('button', [0.5, -2.5, 'Stop animation',function(){r.stopAnimation()}]);
 var c = board.create('circle',['A',function(){return r.Value();}]);
</script>

{lang=EN} Once again we create a board, and add to it a slider named 'r'. This will be the radius of our circle. Then we create point A for the centre. We have already shown how to create a button, we do this with var button1 = board.create('button', [-2, -2.3, 'Start increasing',function(){s.startAnimation(1, 40, 30)}]);. First are the coordinates for the button, then the text on it and lastly is the command. With function(){s.startAnimation(1, 40, 30)}, we start the animation of the slider. This function has 3 parameters:

• direction
• step count
• delay (in milliseconds)

Direction is either +1 or -1, we used one for increasing and the other for decreasing the radius. Step count is in our case 40, this means that the slider is separated into 40 subsections - the bigger the number, the smoother the animation. And lastly the delay is 30 milliseconds, that is how much time passes between moving to the next subsection of the slider. The smaller the number, the faster it moves.

The second button is created in a similar way, the main difference is in the direction and we made the animation less smooth by reducing the step count. The third button is used to stop the animation of the slider, this is done with the function r.stopAnimation(), which doesn't need any parameters.

Then we just have to create a circle with center A and the radius given by the slider. {/lang}

{lang=SI} Spet ustvarimo risalno površino in na njo dodamo drsnik z imenom 'r'. Ta bo predstavljal polmer našega kroga. Potem ustvarimo nevidno točko A, ki bo središče kroga. Naučili smo se že, kako ustvariti gumb, to naredimo z ukazom var button1 = board.create('button', [-2, -2.3, 'Start increasing',function(){s.startAnimation(1, 40, 30)}]);. Tako kot prej moramo najprej zapisate koordinate gumba, napis na njem in ukaz ob kliku. Uporabimo funkcijo function(){s.startAnimation(1, 40, 30)}, ki začne animacijo drsnika. Potebuje tri parametre:

• smer,
• korak,
• zakasnitev (v milisekundah).

Smer je lahko +1 ali -1, eno bomo uporabili za večanje, drugo za manjšanje polmera. Korak je v našem primeru 40, kar pomeni, da je drsnik razdeljen na 40 delov, več delov pomeni bolj tekočo animacijo. Zakasnitev je 30 milisekund, ki predstavlja čas med vsakim premikom na naslednji del drsnika. Manjša kot je številka, hitreje se premika.

Drugi gumb je ustvarjen podobno kot prvi, glavna razlika je v smeri, ki je -1 in v številu korakov na drsniku (ker je korakov manj, je animacija bolj groba). Tretji gumb uporabimo za ustavitev animacije, to storimo s pomočjo funkcije r.stopAnimation(), ki ne potrebuje parametrov.

Potem samo konstruiramo krog s središčem v A in polmerom, ki ga določa drsnik. {/lang}

{lang=CZ} {/lang}

{lang=EN}

Example: Animation with slider

Cycloids. Rolling a circle along a straight line a point firmly connected to its rim draws a curve called a cycloid. If the point is closer to the center a curve drawn by it is called a curtate cycloid. If the point is further from the center than the rim, the resulting curve is called a prolate cycloid, see figure below. Create a dynamic geometry model of the given situation, movement of the circle controlled by the slider. {/lang}

{lang=SI}

Primer: animacija z drsnikom

Cikloida. Če fiksiramo točko na krožnici in krog zakotalimo po ravni podlagi, nam fiksirana točka opiše krivuljo, ki se imenuje
cikloida. Če je točka znotraj kroga, rečemo krivulji skrčena cikloida, če pa je točka zunaj kroga, pa raztegnjena cikloida. Ustvarili bomo dinamično sliko, ki bo narisala cikloido od premikanju drsnika. {/lang}

{lang=CZ}

Příklad: Animace užitím posuvníku

Cykloidy. Při odvalování kruhu podél přímky vykresluje bod pevně spojený s jeho okrajem křivku zvanou cykloida. Pokud je uvažovaný bod blíže ke středu kruhu, než je jeho okraj, jeho trajektorií je křivka zvaná zkrácená cykloida (curtate cycloid). Pokud je předmětný bod dále od středu, než je okraj kruhu, jeho trajektorií je prodloužená cykloida (prolate cycloid). Vytvořte dynamický geometrický model popsaných situací u kterého je pohyb kružnice ovládán posuvníkem, viz níže uvedený obrázek. {/lang}

{lang=EN} Programming:

First, we define dimensions, width and height, of the drawing area setting the corresponding properties of the div element: {/lang}

{lang=SI} Programiranje:

Določimo dimenzije risalne površine: {/lang}

{lang=CZ} Programování:

Nejprve stanovíme rozměry, tj. šířku a výšku, nákresny přiřazením náležitých hodnot odpovídajícím atributům prvku div: {/lang}

<div id="jxgbox" class="jxgbox" style="width:900px; height:300px;"></div>

{lang=EN} Subsequently, at the beginning of the code bounded by the tags <script>, </script>, we determine the Bounding box as follows: {/lang}

{lang=SI} Nadalje določimo bounding box na naslednji način: {/lang}

{lang=CZ} Následně, na začátku kódu vymezeného tagy <script>, </script>, definujeme rozsahy souřadnicových os zavedených v nákresně: {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:250px;"></div>
<script>
    var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-2, 5, 16, -1], axis:false, showClearTraces: true});
</script>

{lang=EN} Note the attribute showClearTraces used above. Setting its value to true displays the button for deleting the traces of points, see the circled x at the bottom of the bounding box.

As the first construction, we draw a straight line MN, a path for the circle: {/lang}

{lang=SI} Opazimo atribut showClearTraces. Če nastavimo njegovo vrednost na true, se ustvari gumb, ki izbriše sled točke (obkrožen $x$ spodaj desno).

Narišemo še premico MN, ki bo predstavljala pot kotaljenja kroga: {/lang}

{lang=CZ} Všimněme si atributu showClearTraces, který je použit ve výše uvedeném příkazu pro iniciaci nákresny. Nastavení jeho hodnoty na true vede k zobrazení užitečného tlačítka pro mazání stop bodů, viz symbol kruhu s křížkem uvnitř při dolním okraji nákresny ve výše uvedeném dynamickém obrázku.

Konstrukci řešení začneme sestrojením přímky MN, cesty pro odvalování kruhu: {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:250px;"></div>
<script>
    var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-2, 5, 16, -1], axis:false, showClearTraces: true});
	var M = board.create('point',[-1,0],{name:'M', face:'o', size:1, visible:false});
    var N = board.create('point',[7,0],{name:'N', face:'o', size:1, visible:false});
    var l1 = board.create('line', [M,N], {color:'black'});
</script>

{lang=EN} Before drawing the circle, we create two sliders to control the values of r, radius of the circle, and l, the amount of translation of the circle center, respectively: {/lang}

{lang=SI} Predno narišemo krog, ustvarimo dva drsnika, ki nadzirata vrednosti polmera r in premika l krožnice po premici . {/lang}

{lang=CZ} Před sestrojením vlastního kruhu vytvoříme dva posuvníky pro ovládání hodnot parametrů r, poloměru kruhu, a l, velikosti posunutí středu kruhu při jeho pohybu: {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:250px;"></div>
<script>
    var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-2, 5, 16, -1], axis:false, showClearTraces: true});
	var M = board.create('point',[-1,0],{name:'M', face:'o', size:1, visible:false});
    var N = board.create('point',[7,0],{name:'N', face:'o', size:1, visible:false});
    var l1 = board.create('line', [M,N], {color:'black'});
	var r = board.create('slider', [[-1, -0.5], [1,-0.5], [0, 1, 3]], {name:'r', snapWidth: 0.1});
    var l = board.create('slider', [[5, -0.5], [10,-0.5], [-2.00, 0, 18.00]], {name:'l', snapWidth: 0.01});
</script>

{lang=EN} Then we proceed to the construction of the circle c with center C and radius r: {/lang}

{lang=SI} Potem nadaljujemo s konstrukcijo kroga c s središčem v C in polmerom r: {/lang}

{lang=CZ} Pokračujeme sestrojením samotného kruhu c se středem C a poloměrem r: {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:250px;"></div>
<script>
    var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-2, 5, 16, -1], axis:false, showClearTraces: true});
	var M = board.create('point',[-1,0],{name:'M', face:'o', size:1, visible:false});
    var N = board.create('point',[7,0],{name:'N', face:'o', size:1, visible:false});
    var l1 = board.create('line', [M,N], {color:'black'});
	var r = board.create('slider', [[-1, -0.5], [1,-0.5], [0, 1, 3]], {name:'r', snapWidth: 0.1});
    var l = board.create('slider', [[5, -0.5], [10,-0.5], [-2.00, 0, 18.00]], {name:'l', snapWidth: 0.01});
	var C = board.create('point', [function(){return l.Value();},function(){return r.Value();}], {color:'blue', size:1, name:'C'});
    var c = board.create('circle', [C,function(){return r.Value();}], {color:'orange', fillOpacity: 0.1});
</script>

{lang=EN} By defining three fixed points A0, B0, C0 with different distances from the circle’s center we contribute to obtaining the above mentioned cycloids; curtate, normal and prolate cycloid, respectively: {/lang}

{lang=SI} Definiramo tri fiksne točke A_0, B_0, C_0, na različnih oddaljenostih od središča kroga, ki nam bodo določale vse tri prej opisane cikloide: {/lang}

{lang=CZ} Definováním následujících tří pevných bodů A0, B0, C0 s různými vzdálenostmi od středu kruhu si připravíme startovní pozice pro získání výše uvedených cykloid; zkrácené, normální a prodloužené cykloidy, v daném pořadí: {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:250px;"></div>
<script>
    var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-2, 5, 16, -1], axis:false, showClearTraces: true});
	var M = board.create('point',[-1,0],{name:'M', face:'o', size:1, visible:false});
    var N = board.create('point',[7,0],{name:'N', face:'o', size:1, visible:false});
    var l1 = board.create('line', [M,N], {color:'black'});
	var r = board.create('slider', [[-1, -0.5], [1,-0.5], [0, 1, 3]], {name:'r', snapWidth: 0.1});
    var l = board.create('slider', [[5, -0.5], [10,-0.5], [-2.00, 0, 18.00]], {name:'l', snapWidth: 0.01});
	var C = board.create('point', [function(){return l.Value();},function(){return r.Value();}], {color:'blue', size:1, name:'C'});
    var c = board.create('circle', [C,function(){return r.Value();}], {color:'orange', fillOpacity: 0.1});
	var A0 = board.create('point', [function(){return C.X();}, function(){return 1.5*r.Value();}], {visible:false});
    var B0 = board.create('point', [function(){return C.X();}, function(){return 2*r.Value();}], {visible:false});
    var D0 = board.create('point', [function(){return C.X();}, function(){return 2.5*r.Value();}], {visible:false});
</script>

{lang=EN} In fact, we will not directly move these points A0, B0, C0, but will create their instant images A, B, C dependent on values that variables controlled by sliders, especially l, can gain: {/lang}

{lang=SI} V resnici ne bomo premikali teh treh točk, ampak bomo ustvarjali njihove kopije glede na vrednosti spremenljivk, ki jih bomo nadzirali z drsnikoma, še posebej z drsnikom l: {/lang}

{lang=CZ} Je třeba říci, že při animaci nepohybujeme přímo s těmito body A0, B0, C0, ale vytváříme jejich okamžité obrazy A, B, C příslušející konkrétním hodnotám proměnných ovládaných posuvníky, především l: {/lang}

<div id="jxgbox" class="jxgbox" style="width:400px; height:250px;"></div>
<script>
    var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-2, 5, 16, -1], axis:false, showClearTraces: true});
	var M = board.create('point',[-1,0],{name:'M', face:'o', size:1, visible:false});
    var N = board.create('point',[7,0],{name:'N', face:'o', size:1, visible:false});
    var l1 = board.create('line', [M,N], {color:'black'});
	var r = board.create('slider', [[-1, -0.5], [1,-0.5], [0, 1, 3]], {name:'r', snapWidth: 0.1});
    var l = board.create('slider', [[5, -0.5], [10,-0.5], [-2.00, 0, 18.00]], {name:'l', snapWidth: 0.01});
	var C = board.create('point', [function(){return l.Value();},function(){return r.Value();}], {color:'blue', size:1, name:'C'});
    var c = board.create('circle', [C,function(){return r.Value();}], {color:'orange', fillOpacity: 0.1});
	var A0 = board.create('point', [function(){return C.X();}, function(){return 1.5*r.Value();}], {visible:false});
    var B0 = board.create('point', [function(){return C.X();}, function(){return 2*r.Value();}], {visible:false});
    var D0 = board.create('point', [function(){return C.X();}, function(){return 2.5*r.Value();}], {visible:false});
	var A = board.create('point',
            [function(){return ((A0.X()-C.X())*Math.cos(l.Value()/r.Value())+(A0.Y()-C.Y())*Math.sin(l.Value()/r.Value()))+C.X();},
             function(){return (-(A0.X()-C.X())*Math.sin(l.Value()/r.Value())+(A0.Y()-C.Y())*Math.cos(l.Value()/r.Value()))+C.Y();}],
            {size:1, color:'red', trace:true});

    var B = board.create('point',
            [function(){return ((B0.X()-C.X())*Math.cos(l.Value()/r.Value())+(B0.Y()-C.Y())*Math.sin(l.Value()/r.Value()))+C.X();},
             function(){return (-(B0.X()-C.X())*Math.sin(l.Value()/r.Value())+(B0.Y()-C.Y())*Math.cos(l.Value()/r.Value()))+C.Y();}],
            {size:1, color:'green', trace:true});

    var D = board.create('point',
            [function(){return ((D0.X()-C.X())*Math.cos(l.Value()/r.Value())+(D0.Y()-C.Y())*Math.sin(l.Value()/r.Value()))+C.X();},
             function(){return (-(D0.X()-C.X())*Math.sin(l.Value()/r.Value())+(D0.Y()-C.Y())*Math.cos(l.Value()/r.Value()))+C.Y();}],
            {size:1, color:'blue', trace:true});
</script>

{lang=EN} The task solution code is now complete. {/lang}

{lang=SI} Koda rešitve je s tem končana. {/lang}

{lang=CZ} Kód řešení úlohy je nyní kompletní. {/lang}

{lang=EN}

Transformations

In JSXGraph it is possible to apply a plane projective transformation to elements using a 3x3 matrix to define the specific transformation. To make life easier JSXGraph has some standard transformations predefined. Some of those are:

• Translation
• Rotation
• Scaling
• Reflection

Translation moves the selected object in the given direction. Scaling increases or decreases the size of our object and rotation rotates it. We will demonstrate some of their uses by constructing a square that can rotate around one vertex. {/lang}

{lang=SI}

Transformacije

V JSXGraphu je možno vpeljati transformacije ravnine na elemente z uporabo matrike velikosti 3x3. Da je postopek malo lažji, ima JSXGraph nekatere standardne transformacije že definirane. Nekatere izmed teh so:

• Translacija
• Rotacija
• Razteg
• Zrcaljenje

Translacija premakne objekt v podani smeri. Razteg poveča ali zmanjša objekt, rotacija pa ga zavrti okoli točke za nek kot. Prikazali bomo njihovo uporabo tako, da bomo konstruirali kvadrat, ki se lahko vrti okoli enega svojega oglišča. {/lang} {lang=CZ} Transformations {/lang}

<div id="jxgbox" class="jxgbox" style="width:500px; height:500px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-4, 4, 4, -4],keepAspectRatio:true, showCopyright:false, showNavigation:false });
 var s = board.create('slider', [[-2,-2],[2,-2],[0,0,2*Math.PI]],{name:'angle'});
 var A = board.create('point', [-1,0], {name:'Drag me', style:5});
 var right = board.create('transform', [2,0], {type:'translate'});
 var up = board.create('transform', [0,2], {type:'translate'});
 var B = board.create('point', [A,right], {name: 'B', style:7});
 var C = board.create('point', [A,[right,up]], {name: 'C', style:7});
 var D = board.create('point', [A,up], {name: 'D', style:7});
 var sq = board.create('polygon', [A,B,C,D]);
 var rot = board.create('transform', [function(){return s.Value();},A], {type:'rotate'});
 rot.bindTo([B,C,D]);
</script>

{lang=EN} Let's now look at the code. The first steps are standard, we create a board and a a slider named 'angle' with values from 0 to 2$\pi$, that we can later use to rotate the square by 360°. Then we create a point called 'Drag me', from which we will construct the other three points of a square.

The next two lines var right = board.create('transform', [2,0], {type:'translate'}); and var up = board.create('transform', [0,2], {type:'translate'}); create our first transformations. The first parameter of any transformation is the text 'transform' and the last parameter is always {type:''}. The second parameter is based on the type of our transformation. In the case of a translation, we need to input a vector [x,y] with either constants or functions as the input. We defined ours with directions [0,2], meaning movement of a point 2 units to the right, and [2,0]; moving 2 units up. Now we can construct the rest of our square:

var B = board.create('point', [A,right], {name: 'B', style:7});
var C = board.create('point', [A,[right,up]], {name: 'C', style:7});
var D = board.create('point', [A,up], {name: 'D', style:7});

We can see that all three points are constructed from the starting point A using the up and right translations. We do this with [A, up] or [A, right]. So to create a new point, we have to input the starting position and then the desired transformation. If we use more that one transformation, we can do this with [A,[right,up]]. We have created 4 points that form a square with the side length 2. Now we just create a polygon var sq using those points.

Next we need to create a rotation. We do this with var rot = board.create('transform', [function(){return s.Value();},A], {type:'rotate'});. We can see that the first and last parameters are similar to the translations, the only difference is of course the type. Since this is a rotation, we have to input the angle and center of the rotation. The input is always in the form of [angle, point]. We do this with [function(){return s.Value();},A]. Notice, that the first parameter is not a constant, but rather a function returning the value of our slider. This way we can influence the angle of the rotation, and the center of the rotation is point A.

Lastly we have to connect our rotation to the square. This will ensure that all point of the square are moving at the same time and at the same angle. We do this with the command rot.bindTo([B,C,D]);. Our transformation is now bound to the points B,C,D (since A is the center of the rotation it does not move, so we dont need to bind it).

For information on other transformations see here. {/lang}

{lang=SI} Poglejmo sedaj konstrukcijo. Prvi koraki so že standardni, ustvarimo risalni prostor in na njem drsnik z imenom 'angle' z vrednostmi od 0 do 2$\pi$, s katerim bomo izvajali rotacijo. Potem dodamo točko z imenom 'Drag me', iz katere bomo s pomočjo translacij konstruirali kvadrat.

Naslednji dve vrstici var right = board.create('transform', [2,0], {type:'translate'}); in var up = board.create('transform', [0,2], {type:'translate'}); definirata naši prvi transformaciji. Prvi parameter katerekoli transformacije je tekst 'transform', zadnji pa je vedno {type:''}. TheDrugi parametri so odvisni od tipa transformacije. V primeru translacije moramo podati vektor oblike [x,y], ki lahko vsebuje konstantne vrednosti, lahko pa ima koordinate izražene s funkcijami. Mi smo definirali smeri kot [0,2], torej premik za dva v desno in [2,0], torej za 2 gor. Zdaj konstruiramo preostanek kvadrata:

var B = board.create('point', [A,right], {name: 'B', style:7});
var C = board.create('point', [A,[right,up]], {name: 'C', style:7});
var D = board.create('point', [A,up], {name: 'D', style:7});

Vidimo, da so vse tri točke dobljene iz začetne točke A z uporabo up in right translacij. To naredimo z zapisom [A, up] ali[A, right]. Torej moramo za konstrukcijo nove točke zapisati začetno točko in transformacijo. Če uporabimo več transformacij, jih zapišemo v seznam kot [A,[right,up]]. Ker smo dobili 4 točke, ki so oglišča kvadrata s stranico 2, lahko definiramo 4-kotnik var sq.

Nato moramo definirati rotacijo var rot = board.create('transform', [function(){return s.Value();},A], {type:'rotate'});. Prvi in zadnji parameter sta podobna kot prej, le da smo uporabili tip 'rotate'. Pri rotaciji sta potrebna center vrtenja in kot vrtenja v obliki [kot, točka]. V našem primeru to pomeni [function(){return s.Value();},A]. Opazimo, da prvi parameter ni konstanta, ampak funkcija, ki vrne vrednost drsnika. Na ta način lahko uporabnik vpliva na vrtenje, središče rotacije pa je točka A.

Za konec moramo še povezati rotacijo s kvadratom. S tem bomo poskrbeli, da se vse točke kvadrata premikajo sočasno in za isti kot. To storimo z ukazom rot.bindTo([B,C,D]);. Transformacija je sedaj vezana na točke B,C,D (ker je A središče vrtenja, se ne premika in ga zato ni potrebno vezati na rotacijo).

Za informacije o ostalih transformacijah glej tukaj. {/lang}

{lang=EN}Advanced topics{/lang}{lang=SI}Advanced topics{/lang}{lang=CZ}Advanced topics{/lang}

{lang=EN}

Adding images

So far we have learned to create many different objects in JSXGraph. In this section we will learn how to include images from the internet onto our drawing board. Transformations can also be used on images, similarly to points or polygons. Let us look at the example below. {/lang}

{lang=SI}

Dodajanje slik

Do sedaj smo ustravili veliko različnih objektov v JSXGraphu. V tem razdelku se bomo naučili, kako na risalno površino vključiti sliko iz interneta. Na slikah lahko uporabljamo tudi transformacije, podobno kot pri točkah ali poligonih. Poglejmo primer. {/lang}

{lang=CZ}Adding images{/lang}

{lang=DE}Bilder einbinden{/lang}

<div id="jxgbox" class="jxgbox" style="width:500px; height:500px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {boundingbox: [-5, -5, 5, 5],
     keepAspectRatio:true, showCopyright:false, showNavigation:false, axis: true });
  var p = board.create('point',[-1,-1], {size:4, opacity:0.5});
  var urlImg = "https://jsxgraph.org/distrib/images/uccellino.jpg";
  var im1 = board.create('image',[urlImg, [0,1], [2,2] ]);
  var im2 = board.create('image',[urlImg, [function(){return p.X();},function(){return p.Y();}], [2,2]], { opacity: 0.6, rotate: 30 });
</script>

{lang=EN} We created a board and bounding box, added the coordinate system and create a point p. With the next line var urlImg = "https://jsxgraph.org/distrib/images/uccellino.jpg"; we saved the URL of our image in the variable urlImg for easier use in the next line.

To create the image, we use var im1 = board.create('image',[urlImg, [0,1], [2,2] ]);. We can see that it takes a list of three parameters. Those are:

• URL of the image (we used the variable, but another way is to write "https://jsxgraph.org/distrib/images/uccellino.jpg"),
• coordinates of the lower left point of the image ([0,1]),
• width and height of the image ([2,2]).

All three parameters can be expressed as functions. In the next line var im2 = board.create('image',[urlImg, [function(){return p.X();},function(){return p.Y();}], [2,2]], { opacity: 0.6, rotate: 30 }); we started the same way, but bound the image to the point p using functions function(){return p.X();}and function(){return p.Y()};. That way if we move the point, the image moves with it.

We also added some attributes {opacity: 0.6, rotate: 30}, the interesting one being rotation. This is similar to a transformation, but this type of rotation only rotates around the lower left point. So if we want to rotate the image around another point, we have to use transformations. For more, see here. {/lang}

{lang=SI} Ustvarili smo površino, bounding box in koordinatni sistem s točko p. Z vrstico var urlImg = "https://jsxgraph.org/distrib/images/uccellino.jpg"; smo shranili URL naslov slike v spremenljivko, ki nam bo pomagala v nadaljevanju.

Za konstrukcije slike zapišemo var im1 = board.create('image',[urlImg, [0,1], [2,2] ]);. Vidimo, da smo zapisali seznam s tremi paramteri. To so:

• URL naslov (tukaj smo uporabili spremeljivko, lahko bi tudi zapisali "https://jsxgraph.org/distrib/images/uccellino.jpg"),
• koordinate spodnje leve točke slike ([0,1]),
• širina in višina slike ([2,2]).

Vsi parametri so lahko zapisani tudi kot funkcije. V naslednji vrstici var im2 = board.create('image',[urlImg, [function(){return p.X();},function(){return p.Y();}], [2,2]], { opacity: 0.6, rotate: 30 }); smo začeli podobno, ampak smo vezali sliko na točko p z ukazoma function(){return p.X();}and function(){return p.Y()};. Na ta način lahko s premikanjem točke premaknemo celotno sliko.

Dodali smo še dva atributa, to sta {opacity: 0.6, rotate: 30}, pri tem je bolj zanimiva rotacija. Ima podoben učinek kot transformacija, vendar gre tukaj vedno za rotacijo okoli spodnje leve točke slike. Torej če želimo rotirati okoli katere druge točke, uporabimo transformacije. Za več primerov, glejte tukaj. {/lang}

{lang=EN}Capture the construction as image{/lang}{lang=SI}Capture the construction as image{/lang}{lang=CZ}Capture the construction as image{/lang}

{lang=EN} JSXGraph offers several possibilities to take a snapshot of a construction. This may be useful for a student who should be enabled to take a screenshot of a construction, but it may also be useful in an e-learning environment where students' solution of an exercise should be stored on a web server in form of a screenshot. {/lang}

{lang=EN}Screenshot button{/lang}

{lang=EN} The easiest way to enable screenshots is to add the screenshot icon ⌘ in the navigation bar of the construction by adding the attribute showScreenshot:true (and showNavigation:true) to the board attributes.

When the user clicks on the ⌘ icon, an image containing the construction will appear over the JSXGraph board. By right clicking on this image the user can download the image. {/lang}

<div id="jxgbox" class="jxgbox" style="width:500px; height:200px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox', {
     boundingbox: [-5, 2, 5, -2],
     keepAspectRatio:true, 
     showCopyright:false,
     showNavigation:true,
     showScreenshot:true });

 var p = board.create('point', [-2,0], {name:"A"});
 var q = board.create('point', [-1,-1], {name:"B"});
 var r = board.create('point', [1,-0.5], {name:"C"});
 var s = board.create('point', [1,1], {name:"D"});
 var t = board.create('point', [-1,1.5], {name:"E"});

 var poly1 = board.create('polygon',[p,q,r,s,t],
                {name:"", withLabel:true});
});
</script>

{lang=EN} There are a few options available:

• scale: scaling factor (default=1)
• type: format of the screenshot image. Default: png
• symbol: Unicode symbol which is shown in the navigation bar. Default: '\u2318'
• css: CSS rules to format the div element containing the screen shot image
• cssButton: CSS rules to format the close button of the div element containing the screen shot image {/lang}

<div id="jxgbox2" class="jxgbox" style="width:500px; height:200px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox2', {
     boundingbox: [-5, 2, 5, -2],
     keepAspectRatio: true, 
     showCopyright: false,
     showNavigation: true, 
     showScreenshot: true,
     screenshot: {
            scale: 3,
            symbol: \u2318
        }
     });
 var p = board.create('point', [-2,0], {name:"A"});
 var q = board.create('point', [-1,-1], {name:"B"});
 var r = board.create('point', [1,-0.5], {name:"C"});
 var s = board.create('point', [1,1], {name:"D"});
 var t = board.create('point', [-1,1.5], {name:"E"});
 var poly1 = board.create('polygon', [p,q,r,s,t], {name:"", withLabel:true});
</script>

{lang=EN}Save to canvas{/lang}

{lang=EN} JSXGraph constructions can be displayed as static image in a canvas element supplied by developer. The following HTML code contains a JSXGraph construction, a button and a canvas element. {/lang}

<div id="jxgbox3" class="jxgbox" 
    style="width:500px; height:200px;"></div>
<p>
<button id="start_save">Save to canvas</button>
<p>
<canvas id="canvas_out" 
    style="width:500px; height:200px; border: solid 2px blue; 
           border-radius:5px">
</canvas>
</p>

{lang=EN} In addition to the JSXGraph construction, an event listener is added to the button with the ID start_save which calls the method board.renderer.dumpToCanvas() with the ID of the canvas element, the width and height of the exported image and a boolean variable if the texts should be displayed, too. {/lang}

 var board = JXG.JSXGraph.initBoard('jxgbox3', {
     boundingbox: [-5, 2, 5, -2],
     keepAspectRatio: true, 
     showCopyright: false,
     showNavigation: true, 
     });
 var p = board.create('point', [-2,0], {name:"A"});
 var q = board.create('point', [-1,-1], {name:"B"});
 var r = board.create('point', [1,-0.5], {name:"C"});
 var s = board.create('point', [1,1], {name:"D"});
 var t = board.create('point', [-1,1.5], {name:"E"});
 var poly1 = board.create('polygon', [p,q,r,s,t], {name:"", withLabel:true});
 document.getElementById('start_save').onclick = function() {
    var withTexts = true;
    board.renderer.dumpToCanvas('canvas_out', 500, 200, withTexts);
 };

Save to canvas

Save as data URI

{lang=EN} The next possibility is to store the construction as data URI. This is the method of choice if a screenshot of a construction should be stored on a web server in e.g. an e-learning environment. The screenhost can be exported as string with the method

    var withTexts = true, txt;
    txt = board.renderer.dumpToDataURI(withTexts);

The data URI will contain the base64 encoded SVG code of the construction. Text elements which are displayed as HTML texts above the construction will be packed into a SVH foreignObject element. Usually, only web browser are able to display the content of these foreignObject elements. {/lang}

 var board = JXG.JSXGraph.initBoard('jxgbox4', {
     boundingbox: [-5, 2, 5, -2],
     keepAspectRatio: true, 
     showCopyright: false,
     showNavigation: true, 
     });
 var p = board.create('point', [-2,0], {name:"A"});
 var q = board.create('point', [-1,-1], {name:"B"});
 var r = board.create('point', [1,-0.5], {name:"C"});
 var s = board.create('point', [1,1], {name:"D"});
 var t = board.create('point', [-1,1.5], {name:"E"});
 var poly1 = board.create('polygon', [p,q,r,s,t], {name:"", withLabel:true});
 document.getElementById('dump_uri').onclick = function() {
    var withTexts = true, txt;
    txt = board.renderer.dumpToDataURI(withTexts);
    document.getElementById('text_out').value = txt;
 };

Save to text

{lang=EN}

Triggers

In JSXGraph we can add functions that happen when a user based event occurs. These events are:

• mouse drag,
• mouseclick,
• hover over,
• hover out,
• doubleclick...

The list of possible event is very large, for all events see here. All events are defined with the method object.on('event', function). Let us look at a few examples. {/lang}

{lang=SI}

Dogodki

V JSXGraph lahko dodamo funkcije, ki se izvedejo, ko uporabnik opravi določeno dejanje. Ta dejanja so:

• poteg z miško,
• klik z miško,
• premik z miško nad objekt,
• premik z miško stran od objekta,
• dvoklik...

Možnih uporabniških vnosov je veliko, za seznam vseh glej tukaj. Vsi dogodki se definirajo z metodo objekt.on('dogodek', funkcija). Poglejmo nekaj primerov. {/lang}

{lang=CZ}Triggers{/lang}

<p id="output">Click in A or hover over B.</p>
<div id="jxgbox" class="jxgbox" style="width:500px; height:200px;"></div>
<script>
 var board = JXG.JSXGraph.initBoard('jxgbox');
 var A = board.create('point',[-2,1], {fixed: true});
 var B = board.create('point',[3,1]);
 A.on('down', function(){q.visit([3,-2],1000,1)});
 B.on('over', function(){document.getElementById('output').innerHTML = "This is point "+this.name;});
 B.on('out', function(){document.getElementById('output').innerHTML = 'Click in A or hover over B.' ;});
</script>

Click on A or hover over B

{lang=SI} Najprej opazimo, da smo na začetku dodali novo vrstico, to je <p id="output">Click on A or hover over B</p>. S tem smo samo pripravili prostor z besedilom, ki ga bomo v nadaljevanju spreminjali. Nato ustvarimo risalno površino in na njej točki A in B. V naslednji vrstici nad prvo točko uporabimo metodo A.on('down', function(){q.visit([3,-2],1000,1)});. Opazimo, da je ime dogodka 'down', kar pomeni klik miške. Torej ob kliku miške se izvede zraven zapisana funkcija visit, ki smo jo že opisali v poglavju 4.1.

V zadnjih dveh vrsticah pa smo zapisali dva dogodka, ki sta oba vezana na točko B. Najprej uporabimo dogodek 'over', ki se zgodi, ko uporabnik premakne miško nad objekt, nato pa dogodek 'down', ki se zgodi, ko uporabnik miško odmakne od objekta. V obeh primerih je zapisana funkcija document.getElementById('output').innerHTML, ki spemeni zapis dokumenta, ki smo za definirali v prvi vrstici kode. Ko smo z miško nad točko B, bo v njem pisalo This is point B, sicer pa bo pisalo Click on A or hover over B. {/lang}

{lang=EN} The first thng we notice, is that we added a line <p id="output">Click on A or hover over B</p> at the beginning. This is used to create a space with text, which we will be able to change. Then we define our board and on it points A and B. In the next line we use the method A.on('down', function(){q.visit([3,-2],1000,1)});. Notice, that the event name is 'down', which represents a mouseclick. This means, that when the user clicks on point A, the function q.visit() is executed. We have already explained what this function does in chapter 4.1.

The final two lines contain two methods bound to pointB. The first one uses event 'over', which happens when the user hovers over the point. Next is event 'down', which happens, when the user moves the mouse away from the point. Both cases contain the function document.getElementById('output').innerHTML. This is used to change the text of our before defined element. The end result is a line of text over our board, which reads This is point B, when hovering over point B, and Click on A or hover over B otherwise. {/lang}

{lang=EN}

JSXGraph and STACK

What is STACK?

STACK is an open-source computer aided assessment system for mathematics and related sciences. Although STACK includes multiple answer types its main focus is on student-provided mathematical expressions. This means that the student's answer to a question can for example be a polynomial or a matrix.

To evaluate mathematical expressions STACK uses the computer algebra system (CAS) Maxima.

The STACK system provides a new question type for Moodle and ILIAS learning environments. STACK can also be integrated to other learning environments via LTI.

This is what a typical STACK question looks like:

🔗 About STACK

• Official Documentation.

• Installation instructions.

• Credits.

STACK questions and JSXGraph

Firstly, we strongly recommend you do not use any HTML-aware (WYSIWYG) editor when working with questions including JSXGraph. Switch to the plain text editor instead to edit the raw HTML.

The key differences

Graphs that do not need to remember their states between page reloads are basically built just like you would do with the official JSXGraph filter. Note however that STACK does not require this filter to be installed as STACK provides its own implementation with some key differences and additional features:

• STACK does not allow you to name the div-container element the graph is stored in. Instead STACK automatically generates an identifier that is then stored in a variable named divid (also boardid since STACK 4.3.3). Thus a JSXGraph Board in STACK is created like this:

  var board = JXG.JSXGraph.initBoard(divid, { ... });
  

  This is done in order to avoid accidental identifier clashing in cases when there are multiple copies of the same question on the same page.

• Instead of traditional div-elements the JSXGraphs in STACK start and end with STACK style question blocks [[jsxgraph]] and [[/jsxgraph]] respectively. You can control the size of the JSXGraph container with the width and height options. For example,

  [[jsxgraph width="450px" height="350px"]]
  

Input bindings

STACK provides a way to reference the input fields of the question and also provides identifiers for these input elements if requested. For example, in order to create an identifier for an input field with the default name ans1 we would refer to it within the question block like this:

[[jsxgraph input-ref-ans1='ans1Ref']]

After doing so there are multiple ways we can work with the input . The most obvious way is to use some of the STACK specific input binding functions.

1. Straightforward binding

With the straightforward binding function stack_jxg.bind_point(ans1Ref, p1) we can bind the coordinates of a JSXGraph point element with the value of the input field ans1.

Example code:

[[jsxgraph input-ref-ans1='ans1Ref']]

var board = JXG.JSXGraph.initBoard(divid, { boundingbox : [-5, 5, 5, -5], axis : true });

var p1 = board.create('point', [-2, -2], { name : 'bound' });
var p2 = board.create('point', [2, 2], { name : 'free' });

stack_jxg.bind_point(ans1Ref, p1);

board.update();

[[/jsxgraph]]

2. Dual binding

There are two different STACK specific functions for representing vectors, lines, circles or anything that can be defined by two points.

The STACK specific function stack_jxg.bind_point_dual(ans1Ref, p1, p2) allows you to bind two points to an input returning their coordinates as a list of lists.

Example code:

[[jsxgraph input-ref-ans1='ans1Ref']]

var board = JXG.JSXGraph.initBoard(divid, { boundingbox : [-5, 5, 5, -5], axis : true });

var p1 = board.create('point', [-2, -2], { name : 'p_1' });
var p2 = board.create('point', [2, 2], { name : 'p_2' });

board.create('segment', [p1, p2], { fixed : true, strokeWidth : 4, strokeOpacity : .6 });

stack_jxg.bind_point_dual(ans1Ref, p1, p2);

board.update();

[[/jsxgraph]]

3. Relative binding

The STACK specific function stack_jxg.bind_point_relative(ans1Ref, p1, p2) works similarly to the aforementioned bind_point_dual function but returns the coordinates of the latter point relative to the initial point, i.e. [p2.X()-p1.X(), p2.Y()-p1.Y()].

Example code:

[[jsxgraph input-ref-ans1='ans1Ref']]

var board = JXG.JSXGraph.initBoard(divid, { keepaspectratio : true, axis : true });

var p1 = board.create('point', [0, 0], { name : 'p_1' });
var p2 = board.create('point', [2, 0], { name : 'p_2' });
var ci = board.create('circle', [p1, p2]);
stack_jxg.bind_point_relative(ans1Ref, p1, p2);

board.update();

[[/jsxgraph]]

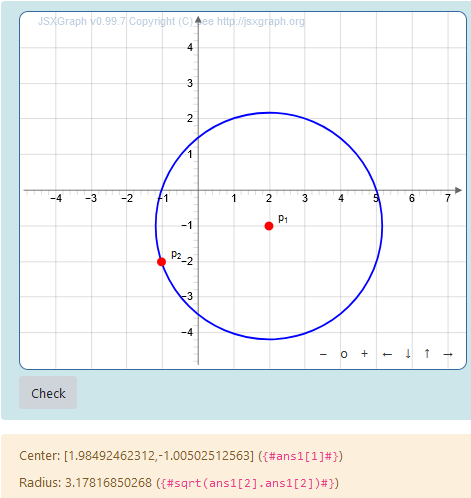
4. Slider binding

It is also possible to bind the value of a slider element with user input using the STACK specific function stack_jxg.bind_slider(ans1Ref, s1).

Example code:

[[jsxgraph width='500px' height='500px' input-ref-ans1='ans1Ref']]

var board = JXG.JSXGraph.initBoard(divid, { boundingbox : [-10, 10, 10, -10], axis : true, shownavigation : false });

var p1 = board.create('point', [0, 0], { name : 'move me!', size : 4, strokeColor : 'black' });
var s1 = board.create('slider', [[3, 8], [8, 8], [1, 4, 7]], { label : 'radius' });

stack_jxg.bind_slider(ans1Ref, s1);

var c1 = board.create('circle', [p1, function() { return s1.Value(); }] , { fillColor : 'orange', fillOpacity : .5 });

board.update();

[[/jsxgraph]]

5. Dynamic binding

As the subject of dynamic binding is rather technical and laborious we won't go into great lengths detailing it here as this is supposed to be a more or less quick introduction. To put it briefly, if your question must have a dynamic number of objects each bound to an input field it is easy to notice that the one-to-one input-object-binding described in the previous examples will not suffice. For more varied data (say you want to store the state of some JavaScript objects, lists, dictionaries etc.) what you can do is to convert the data to JSON strings, which can then be stored into String type input fields. In order to parse this data STACK provides the function stackjson_parse(state).

One way and two way binding

In all of the examples given above we used what is referred to as one way binding, that is to say, the binding transfers some data from the JSXGraph element over to the user input and then retrieves this stored value whenever the page is reloaded.

In addition to this, STACK also uses two way binding which means that we can continue to keep track of the input value even after the page has been loaded so that if its value is changed due to any action, this change is also conveyed into the graph.

As a useful consequence of this feature we can have multiple graphs with objects bound to the same input and have the objects move in sync when some action is performed on any one of them.

{/lang} {lang=SI}JSXGraph and Stack{/lang}{lang=CZ}JSXGraph and Stack{/lang}

Contributors

• Igor Pesek (English and Slovenian version)
• Jaka Hedžet (English and Slovenian versions)
• Roman Hašek (Czech version and Examples)
• Alfred Wassermann (German version)
• other members of ITEMS project